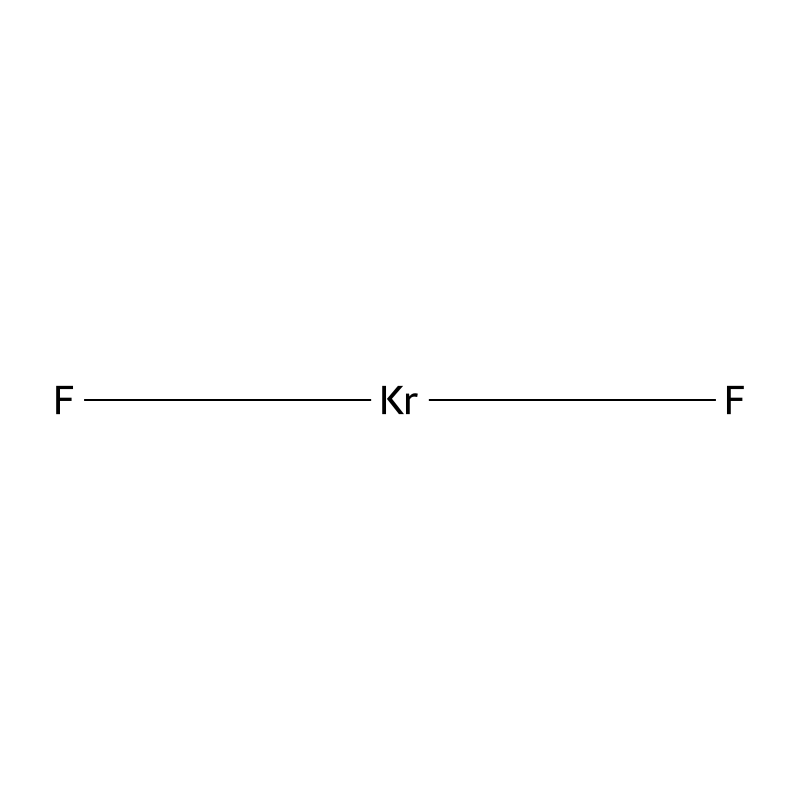
Krypton difluoride
Catalog No.
S1509160
CAS No.
13773-81-4
M.F
F2K
M. Wt
121.79 g/mol
Availability
* This item is exclusively intended for research purposes and is not designed for human therapeutic applications or veterinary use.
Content Navigation
CAS Number
13773-81-4
Product Name
Krypton difluoride
IUPAC Name
difluorokrypton
Molecular Formula
F2K
Molecular Weight
121.79 g/mol
InChI
InChI=1S/F2Kr/c1-3-2
InChI Key
QGOSZQZQVQAYFS-UHFFFAOYSA-N
SMILES
F[Kr]F
Canonical SMILES
F[Kr]F
UNII
A91DJL4OJC
Other CAS
13773-81-4
Wikipedia
Krypton difluoride
General Manufacturing Information
Krypton fluoride (KrF2): INACTIVE
Dates
Modify: 2023-07-17
Explore Compound Types
Get ideal chemicals from 750K+ compounds
CAS No.:68236-13-5
Molecular Formula:C20H20O5
Molecular Weight:340.4 g/mol
Availability:
In Stock
CAS No.:32383-76-9
Molecular Formula:C16H14O4
Molecular Weight:270.28 g/mol
Availability:
In Stock
CAS No.:1189-37-3
Molecular Formula:C19H38O2
Molecular Weight:298.5 g/mol
Availability:
In Stock
CAS No.:4461-52-3
Molecular Formula:C2H6O2
Molecular Weight:62.07 g/mol
Availability:
In Stock
CAS No.:58525-82-9
Molecular Formula:C8H10N2O3
Molecular Weight:182.18 g/mol
Availability:
In Stock
CAS No.:123333-67-5
Molecular Formula:H2NaO3P
Molecular Weight:103.978 g/mol
Availability:
In Stock
