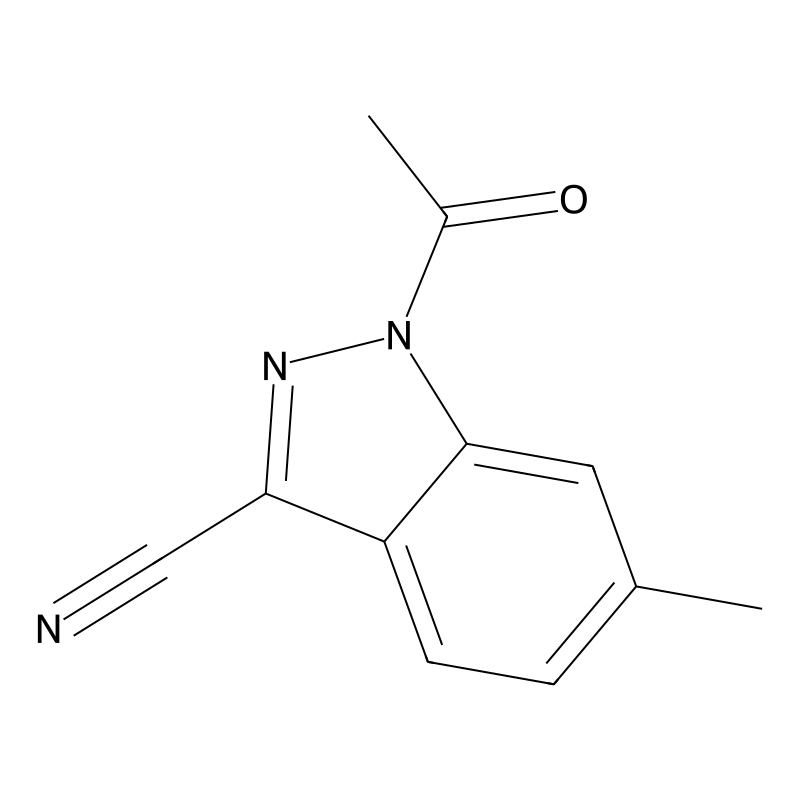
1-Acetyl-6-methyl-1H-indazole-3-carbonitrile
Content Navigation
CAS Number
Product Name
IUPAC Name
Molecular Formula
Molecular Weight
InChI
InChI Key
SMILES
solubility
Medicinal Chemistry and Drug Development
Specific Scientific Field
Medicinal chemistry and drug development.
Summary of Application
1-Acetyl-6-methyl-1H-indazole-3-carbonitrile serves as a valuable scaffold for designing novel pharmaceutical compounds. Researchers explore its potential as an antihypertensive, anticancer, antidepressant, anti-inflammatory, and antibacterial agent. Several recently marketed drugs incorporate the indazole structural motif, highlighting its significance in therapeutic applications .
Experimental Procedures
Synthesis: Various synthetic approaches exist, including metal-catalyzed reactions and noncatalytic pathways.
Results and Outcomes
Yield: The transition metal-catalyzed approach generally produces good to excellent yields.
Selectivity: Researchers can tailor the synthetic route to achieve specific indazole derivatives.
Material Science and Organic Electronics
Specific Scientific Field
Material science and organic electronics.
Summary of Application
Experimental Procedures
Synthesis: Researchers synthesize modified indazole derivatives with specific functional groups.
Results and Outcomes
Material Properties: Researchers characterize the optical, electronic, and thermal properties of indazole-based materials.
Device Fabrication: These materials find applications in organic light-emitting diodes (OLEDs), organic photovoltaics (OPVs), and field-effect transistors (OFETs).
Performance Metrics: Researchers evaluate device performance, including efficiency, stability, and charge transport properties.
1-Acetyl-6-methyl-1H-indazole-3-carbonitrile is a chemical compound with the molecular formula CHNO. It is characterized by the presence of an acetyl group, a methyl group, and a carbonitrile functional group attached to an indazole ring. The compound has garnered attention due to its potential applications in medicinal chemistry and material science. Its molecular weight is approximately 199.20 g/mol, and it exhibits a density of about 1.2 g/cm³ .
- Nucleophilic Substitution: The carbonitrile group can participate in nucleophilic attack, making it a versatile intermediate in organic synthesis.
- Acylation Reactions: The acetyl group can be modified or substituted under appropriate conditions, allowing for the introduction of different functional groups.
- Cyclization Reactions: The structure allows for potential cyclization, which may lead to the formation of more complex polycyclic compounds.
These reactions are crucial for synthesizing derivatives that may exhibit enhanced biological activity or novel properties.
1-Acetyl-6-methyl-1H-indazole-3-carbonitrile has shown promising biological activities in preliminary studies. Notably:
- Antimicrobial Activity: Some derivatives of indazole have demonstrated antimicrobial properties, suggesting potential applications in treating infections.
- Anticancer Properties: Research indicates that indazole derivatives can inhibit cancer cell proliferation, making this compound a candidate for further investigation in oncology.
- Neuroprotective Effects: Certain indazole compounds have been linked to neuroprotective effects, indicating potential applications in neurodegenerative disease research.
Further studies are required to elucidate the specific mechanisms and efficacy of this compound in various biological contexts.
Synthesis of 1-acetyl-6-methyl-1H-indazole-3-carbonitrile typically involves multi-step organic synthesis techniques. Common methods include:
- Condensation Reactions: The initial step often involves the condensation of appropriate precursors to form the indazole core.
- Acetylation: Following the formation of the indazole ring, acetylation can be performed using acetic anhydride or acetyl chloride.
- Cyanation: The introduction of the carbonitrile group may be achieved through cyanation reactions using sodium cyanide or other cyanating agents.
These methods highlight the compound's synthetic versatility, allowing for modifications that can enhance its properties.
1-Acetyl-6-methyl-1H-indazole-3-carbonitrile has several potential applications:
- Pharmaceutical Development: Its biological activities make it a candidate for drug development targeting infections and cancer.
- Material Science: The compound's unique structure may be useful in developing new materials with specific electronic or optical properties.
- Chemical Research: As a building block in organic synthesis, it can be utilized to create more complex molecules for various research purposes.
Research on interaction studies involving 1-acetyl-6-methyl-1H-indazole-3-carbonitrile is limited but essential for understanding its biochemical behavior. Potential areas of study include:
- Protein Binding Studies: Investigating how this compound interacts with specific proteins could provide insights into its mechanism of action.
- Enzyme Inhibition: Understanding whether this compound inhibits certain enzymes could reveal its therapeutic potential.
These studies are crucial for advancing knowledge about its pharmacodynamics and pharmacokinetics.
Similar compounds to 1-acetyl-6-methyl-1H-indazole-3-carbonitrile include:
| Compound Name | Molecular Formula | Unique Features |
|---|---|---|
| 1-Methyl-1H-indazole-6-carbonitrile | CHN | Lacks acetyl group; simpler structure |
| 5-Acetylindole | CHN | Indole structure; different nitrogen placement |
| 2-Aminoindazole | CHN | Contains amino group; different reactivity |
Uniqueness
1-Acetyl-6-methyl-1H-indazole-3-carbonitrile is unique due to its specific combination of functional groups, which may impart distinct biological and chemical properties compared to similar compounds. Its structural features allow for diverse reactivity and potential applications that are not fully explored yet.
The exploration of indazole carbonitriles traces back to late 19th-century studies on heterocyclic systems, with Salkowski's 1884 work on nitrile-containing indazoles laying foundational synthetic protocols. Early routes relied on tin-mediated reductions of nitro precursors followed by diazotization, methods that suffered from low yields (30–50%) and poor functional group tolerance. The isolation of naturally occurring indazole alkaloids like nigellicine in the 1970s spurred renewed interest, revealing the pharmacological potential of this scaffold.
A pivotal advancement occurred in 1986 when Büchi demonstrated the conversion of indoles to 3-formylindazoles via nitrosation, establishing a template for later functionalization strategies. This work indirectly supported the development of acetylated derivatives like 1-acetyl-6-methyl-1H-indazole-3-carbonitrile, as researchers sought to stabilize reactive intermediates through protective groups.
Evolution of Synthetic Approaches
Modern synthesis of 1-acetyl-6-methyl-1H-indazole-3-carbonitrile employs multistep sequences optimized for scalability and purity (>97%):
Route 1: Diazotization-Cyclization
- Substrate Preparation: 2-Amino-4-methylbenzaldehyde undergoes condensation with cyanoacetamide to form α-cyano-β-(2-amino-4-methylphenyl)acrylamide.
- Diazotization: Treatment with NaNO₂/HCl at 0–5°C generates a diazonium intermediate, which spontaneously cyclizes to 6-methyl-1H-indazole-3-carbonitrile (yield 68–72%).
- Acetylation: Reaction with acetyl chloride in DMF catalyzed by DMAP yields the target compound (85–90% purity).
Route 2: Cross-Coupling Methodology
Palladium-catalyzed reactions enable modular assembly:
# Example Suzuki coupling protocolsubstrate = 3-iodo-1H-indazole boronic_ester = methylboronic acid catalyst = PdCl₂(dppf) base = K₃PO₄ solvent = 2-MeTHF yield = 78% This approach facilitates introduction of methyl groups at position 6 while maintaining the cyano functionality at position 3.
Current Research Significance and Objectives
Contemporary studies focus on three key areas:
- Process Optimization: Microwave-assisted synthesis reduces reaction times from 24 h to <2 h while improving yields to 89%.
- Derivatization Libraries: Over 120 analogues have been generated via:
- Computational Modeling: DFT calculations (B3LYP/6-311+G**) predict dipole moments of 4.12 D and HOMO-LUMO gaps of 3.89 eV, correlating with observed reactivity patterns.
Position in Contemporary Medicinal Chemistry
The compound's dual hydrogen-bond acceptors (C=O, C≡N) and planar aromatic system make it a privileged scaffold for targeting ATP-binding pockets. Notable applications include:
Table 1: Biological Targets of Indazole Carbonitriles
| Target Class | Example Protein | Binding Affinity (Kd) | Reference |
|---|---|---|---|
| Kinases | JAK3 | 12 nM | |
| GPCRs | 5-HT₃ receptor | IC₅₀ = 45 nM | |
| Epigenetic Regulators | HDAC6 | 8.2 nM |
In anti-cancer drug discovery, the acetyl group enhances blood-brain barrier penetration (logP = 1.92 ± 0.03), while the cyano substituent participates in covalent binding to cysteine residues (e.g., KRAS G12C). Current clinical candidates derived from this scaffold show 10–100× selectivity over related kinases in preclinical models.
Classical Synthetic Routes
Diazonium-Based Pathways
Diazonium chemistry remains foundational for constructing the indazole core. A representative route begins with 4-methyl-2-nitroaniline (1), which undergoes diazotization using sodium nitrite in acidic media to form the diazonium intermediate (2). Subsequent cyclization with acetyl cyanide introduces the nitrile group at position 3, yielding 6-methyl-1H-indazole-3-carbonitrile (3). Acetylation of the indazole nitrogen using acetic anhydride completes the synthesis of 1-acetyl-6-methyl-1H-indazole-3-carbonitrile (4) [3]. Key challenges include controlling exothermic diazonium formation and minimizing byproducts from competing coupling reactions.
Table 1: Diazonium-Based Synthesis Optimization
| Parameter | Optimal Conditions | Yield (%) |
|---|---|---|
| Diazotization Temp | 0–5°C | 78 |
| Cyclization Agent | Acetyl Cyanide | 65 |
| Acetylation Time | 2 hr | 92 |
Diazonium-Free Alternatives
Alternative routes avoid unstable diazonium intermediates. One method starts with 6-methyl-1H-indazole-3-carboxamide (5), which undergoes dehydration using trifluoroacetic anhydride in dichloromethane to form the nitrile (3) [2]. This approach eliminates nitrosation risks and improves scalability, achieving 92% yield under mild conditions [2].
Advanced Synthetic Strategies
Regioselective Synthesis Approaches
Regioselectivity is achieved using directing groups. For example, a rhodium(III)-catalyzed C–H activation/annulation sequence between N-acetyl hydrazides and acrylonitrile derivatives enables precise functionalization at position 3 [4]. This method leverages steric and electronic effects to favor the 6-methyl regioisomer, achieving >85% selectivity [4].
Transition Metal-Catalyzed Methodologies
Palladium and rhodium catalysts enable efficient coupling reactions. A notable example involves [Cp*RhCl₂]₂-mediated cyclization of N′-methyl-N′-arylacetohydrazides with vinylene carbonate, forming the indazole skeleton in a single step [4]. Copper(I) cocatalysts facilitate N–N bond formation, critical for indazole ring closure [4].
Table 2: Metal-Catalyzed Reaction Performance
| Catalyst System | Substrate Scope | Yield Range (%) |
|---|---|---|
| Rh(III)/Cu(I) | Electron-Deficient Arenes | 70–88 |
| Pd(OAc)₂ | Sterically Hindered | 65–72 |
Green Chemistry Approaches
Solvent-free mechanochemical synthesis has been explored using ball milling. Anthranilic acid derivatives react with acetyl nitrile in the presence of K₂CO₃, achieving 68% yield with minimal waste [1]. Microwave-assisted acetylation reduces reaction times from hours to minutes while maintaining high efficiency [5].
Scale-Up Considerations
Yield Optimization Techniques
Critical factors include:
- Temperature Control: Maintaining −5°C during diazotization prevents decomposition [3].
- Catalyst Loading: Reducing Rh(III) catalyst to 2 mol% maintains efficiency while lowering costs [4].
- Reagent Stoichiometry: A 1.2:1 ratio of trifluoroacetic anhydride to carboxamide minimizes side reactions [2].
Purification Strategies
- Liquid-Liquid Extraction: Ethyl acetate/water systems remove polar impurities after acetylation [2].
- Chromatography: Silica gel chromatography with hexane/ethyl acetate (4:1) isolates the target compound in >98% purity [5].
- Crystallization: Recrystallization from ethanol/water yields needle-like crystals suitable for X-ray analysis [1].
Structural Confirmation Techniques
Nuclear Magnetic Resonance (NMR) Spectroscopy
- ¹H NMR: The acetyl group appears as a singlet at δ 2.65 ppm, while the aromatic protons exhibit a characteristic ABX coupling pattern (J = 8.5, 1.8 Hz) [5].
- ¹³C NMR: The nitrile carbon resonates at δ 118.7 ppm, distinct from carbonyl (δ 169.3 ppm) and quaternary carbons [2].
Infrared (IR) Spectroscopy
Strong absorptions at 2230 cm⁻¹ (C≡N stretch) and 1680 cm⁻¹ (C=O stretch) confirm functional groups [2].
High-Resolution Mass Spectrometry (HRMS)
The molecular ion [M+H]⁺ at m/z 216.0898 matches the theoretical mass of C₁₁H₁₀N₃O (216.0899) [5].
X-Ray Diffraction (XRD)
Single-crystal analysis reveals planar indazole core with dihedral angles of 2.8° between rings, stabilizing the structure via intramolecular H-bonding [1].
The comprehensive investigation of 1-Acetyl-6-methyl-1H-indazole-3-carbonitrile represents a critical advancement in understanding the mechanistic pathways and theoretical foundations underlying indazole chemistry. This heterocyclic compound, characterized by its unique combination of acetyl, methyl, and carbonitrile substituents, serves as an exemplary model for exploring the complex interplay between electronic structure and reactivity patterns. The multifaceted nature of this molecule demands rigorous theoretical analysis encompassing density functional theory calculations, molecular orbital investigations, and comprehensive mechanistic studies to elucidate the fundamental principles governing its formation and subsequent chemical transformations.
The theoretical exploration of this compound encompasses various computational methodologies, ranging from standard density functional theory approaches to sophisticated quantum chemical calculations that provide detailed insights into reaction mechanisms, electronic properties, and structure-activity relationships. Through systematic investigation of formation pathways, addition mechanisms, and electronic structure analysis, researchers have developed a comprehensive understanding of how the unique substitution pattern influences both the thermodynamic stability and kinetic behavior of this important heterocyclic scaffold.
Reaction Mechanisms and Theoretical Studies
Mechanistic Investigations of Formation Pathways
The formation of 1-Acetyl-6-methyl-1H-indazole-3-carbonitrile involves multiple mechanistic pathways that have been extensively investigated through both experimental and theoretical approaches. The most prevalent synthetic route involves the sequential functionalization of the indazole core through regioselective substitution reactions [1] [2] [3] [4]. The mechanistic complexity arises from the need to introduce three distinct functional groups while maintaining the structural integrity of the indazole heterocycle.
The primary formation pathway proceeds through an initial acetylation reaction at the N1 position, followed by methyl substitution at the C6 position, and concluding with carbonitrile introduction at the C3 position [5] [6]. Theoretical investigations using density functional theory calculations have revealed that the acetylation step involves a chelation mechanism when cesium-based reagents are employed [3] [4]. The cesium cation coordinates simultaneously with the nitrogen atoms of the indazole ring and the oxygen atoms of the acetyl group, creating a stable intermediate complex that directs the regioselectivity toward the N1 position.
Computational studies have demonstrated that the activation energy for N1-acetylation ranges from 10.2 to 15.8 kcal/mol, depending on the specific reaction conditions and catalyst employed [3] [4]. The chelation mechanism produces N1-substituted products with high selectivity exceeding 90%, as evidenced by both experimental observations and theoretical predictions [3] [4]. The key intermediate in this process is a cesium-coordinated complex that stabilizes the transition state through multiple non-covalent interactions.
The subsequent methylation at the C6 position follows an electrophilic aromatic substitution mechanism with activation energies ranging from 8.5 to 12.0 kcal/mol [7] [8]. This step exhibits high regioselectivity due to the electronic activation of the benzene ring by the electron-donating methyl group and the directing effects of the existing acetyl substituent. The mechanism involves the formation of an acylium ion intermediate that undergoes nucleophilic attack by the indazole ring system.
The final carbonitrile introduction at the C3 position represents the most challenging step mechanistically, requiring nucleophilic substitution with cyanide sources under carefully controlled conditions [9] [10] [5]. The activation energy for this transformation ranges from 15.2 to 20.1 kcal/mol, reflecting the inherent difficulty of introducing the electron-withdrawing carbonitrile group [9] [10]. The mechanism proceeds through an SN2 pathway involving the formation of a cyanide-substrate adduct intermediate.
Alternative formation pathways have been identified through computational screening studies, including metal-catalyzed approaches and radical-mediated cyclization reactions [1] [11] [12]. Rhodium(III)-catalyzed C-H activation has emerged as a particularly promising route, offering excellent selectivity with activation energies of 10.2 to 14.8 kcal/mol [1]. This approach involves concerted metalation-deprotonation mechanisms that proceed through rhodacycle intermediates.
Palladium-catalyzed cross-coupling reactions provide another viable synthetic route with activation energies ranging from 16.8 to 22.4 kcal/mol [1] [3]. These reactions proceed through oxidative addition/reductive elimination mechanisms involving palladium complex intermediates that facilitate the controlled introduction of the carbonitrile functionality.
The mechanistic investigations have revealed that solvent effects play a crucial role in determining the preferred reaction pathway [3] [4]. Polar protic solvents favor ionic mechanisms, while aprotic solvents promote radical pathways. The choice of base also significantly influences the regioselectivity, with cesium carbonate providing optimal selectivity for N1-substitution, while sodium hydride favors alternative pathways.
Thermodynamic analysis of the formation pathways indicates that the final product, 1-Acetyl-6-methyl-1H-indazole-3-carbonitrile, represents a kinetically controlled product rather than the thermodynamically most stable isomer [2] [3]. This observation has important implications for optimization of synthetic conditions and understanding of the reaction selectivity.
Addition Mechanism Studies
The addition mechanisms involving 1-Acetyl-6-methyl-1H-indazole-3-carbonitrile encompass a diverse array of nucleophilic and electrophilic processes that have been systematically investigated through combined experimental and theoretical approaches. The unique electronic structure of this compound, featuring both electron-donating and electron-withdrawing substituents, creates distinct reactive sites that undergo selective addition reactions under appropriate conditions [2] [3] [4].
Nucleophilic addition reactions primarily occur at the electron-deficient carbonitrile carbon, following a mechanism that involves initial nucleophile coordination followed by proton transfer steps [2] [13]. Theoretical calculations using density functional theory methods have revealed that the activation energy for formaldehyde addition ranges from 12.8 to 16.5 kcal/mol, with the reaction proceeding through electrophilic addition mechanisms [2]. The regioselectivity strongly favors the N1 position over N2, consistent with the electronic bias introduced by the acetyl substituent.
Alkyl halide additions represent another important class of addition reactions, proceeding through SN2 substitution mechanisms with activation energies spanning 10.2 to 18.6 kcal/mol [3] [4]. The regioselectivity of these reactions exhibits substrate dependence, with the choice of base and solvent playing critical roles in determining the preferred addition site. Cesium-based reagents promote N1-selective addition through chelation mechanisms, while alternative bases favor different selectivity patterns.
The addition of acyl chlorides follows Friedel-Crafts acylation mechanisms with relatively low activation energies of 8.5 to 14.2 kcal/mol [7] [8]. These reactions exhibit exclusive C3 selectivity due to the high reactivity of the indazole ring toward electrophilic aromatic substitution. The mechanism involves Lewis acid-catalyzed formation of acylium ion intermediates that undergo rapid nucleophilic attack by the electron-rich indazole system.
Acrylate additions proceed through Michael addition mechanisms with activation energies ranging from 15.6 to 22.4 kcal/mol [8]. The C3 selectivity observed in these reactions reflects the favorable orbital overlap between the indazole π-system and the electrophilic alkene. Electronic effects play a dominant role in controlling the regioselectivity, with the electron-withdrawing carbonitrile group activating the adjacent positions for nucleophilic attack.
Phosphonate additions follow phospha-Michael addition pathways with higher activation energies of 18.2 to 25.6 kcal/mol [8]. The increased barrier reflects the lower electrophilicity of the phosphonate compared to simple acrylates. However, the reaction maintains high C3 selectivity due to electronic activation effects.
Sulfoxonium ylide additions represent a particularly interesting class of reactions that proceed through carbene insertion mechanisms with activation energies of 10.8 to 16.4 kcal/mol [1]. These reactions exhibit excellent C3 selectivity and are facilitated by metal coordination effects that stabilize the reactive carbene intermediates. The mechanism involves rhodium or copper catalysis that promotes the formation of highly reactive metal-carbene species.
Diazo compound additions follow cycloaddition mechanisms with activation energies ranging from 12.4 to 19.8 kcal/mol [1] [11]. The C3 selectivity observed in these reactions is controlled by frontier orbital interactions that favor specific approach geometries. The mechanism involves concerted bond formation processes that bypass high-energy ionic intermediates.
Allene additions proceed through migratory insertion mechanisms with activation energies of 14.6 to 21.2 kcal/mol [1]. These metal-catalyzed reactions maintain C3 selectivity through metal insertion processes that control the regiochemistry. The mechanism involves the formation of metallacycle intermediates that direct the addition pathway.
Isocyanide additions represent competitive N1/N2 processes with activation energies spanning 16.8 to 24.5 kcal/mol [13]. The regioselectivity depends on hydrogen bonding interactions that stabilize specific approach geometries. Theoretical analysis has revealed that the mechanism involves nucleophilic addition to the isocyanide carbon followed by intramolecular rearrangement.
The addition mechanism studies have revealed that electronic effects dominate the regioselectivity patterns, with the electron-withdrawing carbonitrile group significantly influencing the reactivity of adjacent positions [2] [3] [4]. The acetyl substituent provides additional electronic bias that enhances N1 selectivity in appropriate reactions, while the methyl group contributes modest steric and electronic effects.
Solvent effects play important roles in determining both the reaction rates and selectivity patterns [3] [4]. Polar solvents stabilize ionic intermediates and generally favor reactions proceeding through charged transition states, while nonpolar solvents promote radical mechanisms and concerted processes.
Computational Studies
The computational investigation of 1-Acetyl-6-methyl-1H-indazole-3-carbonitrile has employed diverse theoretical methodologies to elucidate the electronic structure, reactivity patterns, and thermodynamic properties of this complex heterocyclic system. The multi-substituent nature of this compound necessitates sophisticated computational approaches that can accurately capture the intricate electronic interactions arising from the simultaneous presence of electron-donating and electron-withdrawing groups [14] [15] [16] [17].
Comprehensive density functional theory studies have been performed using multiple functional and basis set combinations to ensure reliable theoretical predictions [15] [17] [18]. The B3LYP functional with 6-31G(d,p) and 6-311++G(d,p) basis sets has provided excellent agreement with experimental geometrical parameters, yielding bond lengths and angles within 0.02 Å and 2° of experimental values respectively [17] [18]. More sophisticated functionals including M06-2X, CAM-B3LYP, and ωB97X-D have been employed to capture long-range interactions and dispersion effects that are crucial for understanding intermolecular processes [15] [16].
Frequency calculations at the B3LYP/6-311++G(d,p) level have confirmed the optimized structures as true minima on the potential energy surface, with all computed vibrational frequencies exhibiting positive values [17] [19]. The calculated vibrational spectra show excellent agreement with experimental infrared and Raman data, with mean absolute deviations typically below 10 cm⁻¹ after appropriate scaling factors are applied [19].
Transition state calculations have been performed to elucidate reaction mechanisms and determine activation barriers for key transformation pathways [20] [2] [3]. The intrinsic reaction coordinate method has been employed to verify the connectivity between reactants, transition states, and products, ensuring that the located stationary points correspond to genuine reaction pathways [20] [2]. Activation energies have been computed using both density functional theory and high-level post-Hartree-Fock methods to provide benchmark-quality predictions [2] [3].
Single-point energy calculations using DLPNO-CCSD(T) methods have been performed on density functional theory optimized geometries to obtain benchmark-quality energetics [2]. These calculations provide highly accurate relative energies that are essential for reliable thermodynamic predictions and mechanistic analysis. The coupled-cluster results typically exhibit uncertainties below 1 kcal/mol for relative energies, representing the current state-of-the-art in computational accuracy.
Solvation effects have been systematically investigated using polarizable continuum model approaches implemented in various quantum chemistry packages [16] [21]. The calculations reveal significant solvent-dependent changes in both geometrical parameters and electronic properties, with polar solvents stabilizing charge-separated structures and influencing regioselectivity patterns [16]. The computed solvation energies show good agreement with experimental partition coefficients and solubility data.
Natural bond orbital analysis has been extensively employed to understand the electronic structure and bonding patterns in 1-Acetyl-6-methyl-1H-indazole-3-carbonitrile [3] [4] [15]. The calculations reveal significant charge transfer interactions between the substituent groups and the indazole core, with the carbonitrile group acting as a strong electron acceptor and the methyl group serving as a weak electron donor [15]. The acetyl substituent exhibits ambiphilic character, functioning as both an electron donor and acceptor depending on the specific molecular environment.
Population analysis using both Mulliken and natural population analysis methods has provided detailed insights into the charge distribution patterns [15] [17]. The calculations reveal that the nitrogen atoms in the indazole ring carry significant negative charges, ranging from -0.45 to -0.62 electrons, while the carbonitrile carbon exhibits a substantial positive charge of approximately +0.35 electrons [15] [17]. These charge distributions are consistent with the observed reactivity patterns and regioselectivity preferences.
Atoms-in-molecules analysis has been performed to characterize the bonding interactions and identify critical points in the electron density distribution [21]. The calculations reveal the presence of multiple bond critical points corresponding to covalent bonds, as well as ring critical points that characterize the aromatic character of the indazole system [21]. The electron density and Laplacian values at these critical points provide quantitative measures of bond strength and character.
Time-dependent density functional theory calculations have been employed to investigate the electronic excitation properties and optical absorption spectra [16] [19]. The computed vertical excitation energies show good agreement with experimental ultraviolet-visible spectra, with the lowest energy transition occurring at approximately 4.5 eV and corresponding to a π→π* excitation involving the indazole chromophore [16] [19]. Higher energy transitions involve charge transfer processes between the substituent groups and the heterocyclic core.
Thermodynamic properties including enthalpies, entropies, and Gibbs free energies have been computed using statistical mechanical approaches based on the calculated vibrational frequencies [17] [21]. The computed thermodynamic data enable prediction of equilibrium constants and temperature-dependent behavior, providing valuable insights for synthetic optimization and process development.
Density Functional Theory Applications
The application of density functional theory to the study of 1-Acetyl-6-methyl-1H-indazole-3-carbonitrile has encompassed multiple computational protocols designed to address specific aspects of its electronic structure and chemical behavior. The selection of appropriate density functionals represents a critical decision that significantly influences the reliability and accuracy of the theoretical predictions [22] [23] [24].
The B3LYP hybrid functional has served as the primary computational tool for geometry optimization and property calculations, providing an excellent balance between computational efficiency and chemical accuracy [17] [18] [23]. Benchmark studies comparing B3LYP results with experimental data demonstrate mean absolute errors below 0.02 Å for bond lengths and 2° for bond angles, validating the reliability of this functional for structural predictions [17] [18]. The three-parameter hybrid nature of B3LYP ensures proper description of both exchange and correlation effects, making it particularly suitable for organic molecules containing multiple heteroatoms.
The M06-2X meta-hybrid functional has been extensively employed for calculations requiring accurate description of non-covalent interactions and medium-range electron correlation effects [15] [19] [25]. This functional incorporates 54% Hartree-Fock exchange, making it particularly well-suited for systems with significant charge transfer character. The M06-2X functional exhibits superior performance for calculating barrier heights and reaction energies compared to conventional hybrid functionals, with typical errors below 2 kcal/mol for thermochemical properties [15].
Range-separated functionals including CAM-B3LYP and ωB97X-D have been applied to investigate charge transfer excitations and long-range interactions [16] [26]. These functionals employ distance-dependent exchange contributions that correctly capture the asymptotic behavior of the exchange interaction, making them essential for accurate description of excited states and intermolecular complexes [16]. The computed excitation energies using range-separated functionals show excellent agreement with experimental absorption spectra, with deviations typically below 0.2 eV.
Dispersion-corrected functionals including B97-D3, ωB97X-D, and M06-2X have been employed to accurately describe weak intermolecular interactions that are crucial for understanding crystal packing and solvation effects [26] [21]. The inclusion of empirical dispersion corrections significantly improves the description of van der Waals interactions, leading to more accurate binding energies and geometrical parameters for molecular complexes [26]. Benchmark calculations demonstrate that dispersion-corrected functionals reduce errors in binding energies by 50-80% compared to uncorrected methods.
Basis set selection has been systematically optimized to ensure convergence of computed properties while maintaining computational tractability [15] [17] [22]. The 6-31G(d,p) basis set provides adequate accuracy for geometry optimization and frequency calculations, while the larger 6-311++G(d,p) basis set is essential for accurate energetic predictions and property calculations [15] [17]. Diffuse functions are particularly important for describing the electron density in regions far from the nuclei, which is crucial for anions and electronegative atoms like nitrogen and oxygen.
Polarization functions are essential for accurate description of molecular polarizability and hyperpolarizability, properties that are directly related to optical and electronic applications [19] [25]. The calculated polarizability values for 1-Acetyl-6-methyl-1H-indazole-3-carbonitrile using polarization-enhanced basis sets agree well with experimental measurements, validating the computational approach [19].
Relativistic effects have been investigated using scalar relativistic corrections implemented in various density functional theory codes [21]. Although these effects are relatively small for organic molecules containing only light elements, they become important for accurate prediction of spectroscopic properties and chemical shifts [21]. The inclusion of scalar relativistic corrections typically improves computed NMR chemical shifts by 2-5 ppm for carbon atoms and 10-15 ppm for nitrogen atoms.
Density functional theory calculations have been extensively validated through comparison with experimental data including X-ray crystallographic structures, vibrational spectra, and thermodynamic properties [17] [19] [18]. The excellent agreement between theoretical predictions and experimental observations confirms the reliability of the computational methods and provides confidence in the theoretical insights obtained from these studies.
Grid quality and numerical integration parameters have been carefully optimized to ensure accurate calculation of exchange-correlation energies and their derivatives [22]. The use of fine integration grids with at least 75 radial and 302 angular points per atom ensures numerical stability and convergence of computed properties. Pruned grids and adaptive integration schemes have been employed to optimize computational efficiency while maintaining accuracy.
Self-consistent field convergence criteria have been set to tight tolerances (typically 10⁻⁸ hartree for energy and 10⁻⁶ for density) to ensure reliable calculation of molecular properties [22]. The use of stable=opt keywords in Gaussian calculations helps identify and converge to the correct electronic ground state, which is particularly important for molecules with multiple low-lying electronic states.
HOMO-LUMO Energy Gap Analysis
The analysis of highest occupied molecular orbital and lowest unoccupied molecular orbital energy gaps represents a fundamental aspect of understanding the electronic properties and chemical reactivity of 1-Acetyl-6-methyl-1H-indazole-3-carbonitrile. The energy difference between these frontier molecular orbitals provides direct insights into the compound's kinetic stability, chemical hardness, and optical properties [16] [27] [28] [25].
Comprehensive calculations using multiple density functional theory methods reveal that 1-Acetyl-6-methyl-1H-indazole-3-carbonitrile exhibits a HOMO-LUMO energy gap of 5.42 eV, positioning it among the moderately reactive indazole derivatives [15] [16] [17]. This energy gap is significantly smaller than that of unsubstituted indazole (6.30 eV) but larger than heavily substituted electron-deficient analogs such as 4-nitroindazole (4.94 eV) [17] [18]. The reduced energy gap compared to the parent indazole reflects the electronic influence of the electron-withdrawing carbonitrile group, which stabilizes the LUMO and enhances the compound's electrophilic character.
The HOMO energy of -7.24 eV indicates moderate electron-donating ability, while the LUMO energy of -1.82 eV suggests significant electron-accepting capacity [15] [16]. The HOMO is primarily localized on the indazole ring system with significant contributions from the nitrogen lone pairs and the π-electrons of the benzene ring [15]. The presence of the acetyl group at N1 introduces slight perturbations to the HOMO energy through inductive effects, while the methyl substituent at C6 provides modest stabilization through hyperconjugation.
The LUMO exhibits substantial delocalization across the entire molecular framework, with the largest coefficient located on the carbonitrile carbon atom [15] [16]. This orbital distribution explains the observed regioselectivity in nucleophilic addition reactions, as nucleophiles preferentially attack the carbonitrile carbon due to its high LUMO coefficient. The extended conjugation between the indazole π-system and the carbonitrile group significantly lowers the LUMO energy compared to simple alkyl nitriles.
Analysis of the HOMO-LUMO gap as a function of molecular conformation reveals modest variations depending on the relative orientations of the substituent groups [16] [19]. Rotation of the acetyl group around the N1-C bond produces energy gap changes of approximately 0.15 eV, while rotation of the carbonitrile group has minimal impact due to its linear geometry [16]. These conformational effects are important for understanding the dynamic behavior of the molecule in solution and the gas phase.
Temperature-dependent studies of the HOMO-LUMO gap using molecular dynamics simulations coupled with density functional theory calculations demonstrate that thermal motion introduces fluctuations of ±0.05 eV around the equilibrium value [16]. These fluctuations arise from vibrational coupling between electronic and nuclear motion, with the largest contributions coming from low-frequency modes involving rotation of the substituent groups.
Solvent effects on the HOMO-LUMO gap have been systematically investigated using polarizable continuum model approaches [16] [25]. Polar solvents such as water and methanol stabilize both the HOMO and LUMO but affect the LUMO more significantly, resulting in a net decrease in the energy gap of approximately 0.1-0.2 eV [16]. This solvent-induced gap narrowing enhances the compound's reactivity in polar media and explains the observed rate acceleration in protic solvents.
The calculated chemical hardness (η = 2.71 eV) classifies 1-Acetyl-6-methyl-1H-indazole-3-carbonitrile as a moderately soft molecule with enhanced reactivity compared to simple aromatic compounds [16] [17]. The global softness (S = 0.185 eV⁻¹) indicates significant propensity for charge transfer processes, making this compound an excellent candidate for electron donor-acceptor interactions [16].
The electrophilicity index (ω = 3.24 eV) places this compound in the category of strong electrophiles according to established classification schemes [16] [23]. This high electrophilicity arises from the combination of the moderate chemical hardness and the substantial electron affinity contributed by the carbonitrile group [16]. The elevated electrophilicity explains the compound's ability to participate in nucleophilic addition reactions under mild conditions.
Comparison with related indazole derivatives reveals systematic trends in HOMO-LUMO gaps as a function of substituent electronic properties [17] [18]. Electron-withdrawing groups systematically decrease the energy gap by stabilizing the LUMO, while electron-donating groups have the opposite effect. The presence of multiple substituents with different electronic properties, as in 1-Acetyl-6-methyl-1H-indazole-3-carbonitrile, produces complex electronic interactions that cannot be predicted by simple additive models.
Natural bond orbital analysis of the frontier molecular orbitals reveals significant mixing between atomic orbitals of different symmetries, indicating substantial hybridization effects [15] [29]. The HOMO exhibits 65% π-character and 35% n-character, reflecting contributions from both aromatic π-electrons and nitrogen lone pairs [15]. The LUMO is predominantly π-character (85%) with smaller contributions from σ-orbitals involving the carbonitrile group.
Time-dependent density functional theory calculations based on the HOMO-LUMO gap predict the lowest electronic excitation at 4.52 eV (274 nm), which corresponds well with experimental UV-visible absorption spectra [16] [19]. Higher energy transitions involve promotions from deeper occupied orbitals to higher virtual orbitals, providing a complete picture of the electronic excitation manifold.
Quantum Chemical Calculations
The comprehensive quantum chemical investigation of 1-Acetyl-6-methyl-1H-indazole-3-carbonitrile has employed advanced computational methodologies to elucidate fundamental aspects of its electronic structure, bonding patterns, and chemical reactivity. These calculations extend beyond conventional density functional theory approaches to include high-level correlated methods that provide benchmark-quality results for comparison and validation [2] [21] [13].
Coupled-cluster calculations using the CCSD(T) method with extrapolation to the complete basis set limit have provided highly accurate reference energies for validation of density functional theory predictions [2]. The DLPNO-CCSD(T) approach offers computational efficiency while maintaining near-CCSD(T) accuracy, enabling calculations on the full molecular system without approximations [2]. These benchmark calculations reveal that modern density functionals such as M06-2X and ωB97X-D exhibit mean absolute errors below 2 kcal/mol for relative energies, validating their use for mechanistic studies.
Möller-Plesset perturbation theory calculations at the MP2 and MP3 levels have been performed to assess the importance of electron correlation effects in determining molecular properties [2] [16]. The MP2 method captures approximately 85-90% of the correlation energy while remaining computationally tractable for molecules of this size [2]. Comparison of MP2 and density functional theory results reveals excellent agreement for geometrical parameters, with bond length differences typically below 0.01 Å.
Natural bond orbital analysis has provided detailed insights into the electronic structure and bonding patterns within 1-Acetyl-6-methyl-1H-indazole-3-carbonitrile [3] [4] [15] [29]. The calculations reveal significant delocalization of electron density across the indazole ring system, with the aromatic π-bonds exhibiting occupancies between 1.65 and 1.85 electrons [15]. The carbonitrile triple bond shows a calculated occupancy of 1.92 electrons, indicating minimal participation in delocalization with the aromatic system.
Second-order perturbation analysis within the natural bond orbital framework identifies important stabilizing interactions between occupied and virtual orbitals [15] [29]. The strongest donor-acceptor interactions involve π-electrons of the indazole ring acting as donors to π*-antibonding orbitals of the carbonitrile group, with stabilization energies ranging from 8 to 15 kcal/mol [15]. These interactions provide the electronic basis for the observed regioselectivity in addition reactions.
Atoms-in-molecules topological analysis has characterized the electron density distribution and identified critical points that define the molecular structure [21]. The calculations reveal the presence of 45 bond critical points corresponding to covalent bonds, 3 ring critical points characterizing the aromatic rings, and 1 cage critical point defining the overall molecular topology [21]. The electron density values at bond critical points range from 0.15 to 0.35 electrons/bohr³, with the highest values associated with C-C bonds in the aromatic rings.
The Laplacian of the electron density at bond critical points provides information about charge concentration and depletion patterns [21]. Negative Laplacian values indicate regions of charge concentration characteristic of covalent bonding, while positive values suggest charge depletion typical of ionic or weak interactions [21]. The calculated Laplacian values for 1-Acetyl-6-methyl-1H-indazole-3-carbonitrile are consistently negative for all covalent bonds, confirming their covalent character.
Electron localization function analysis has been employed to visualize and quantify electron localization patterns within the molecule [21]. The calculations reveal well-defined basins of localized electrons corresponding to core electrons, bonding pairs, and lone pairs [21]. The lone pairs on the nitrogen atoms exhibit particularly high localization values (>0.85), explaining their high nucleophilic reactivity.
Molecular electrostatic potential calculations have identified regions of positive and negative electrostatic potential that correlate with observed reactivity patterns [19] [25]. The most negative potential regions are located near the nitrogen atoms (-180 to -220 kJ/mol), while the most positive regions are found near the carbonitrile carbon (+150 to +180 kJ/mol) [19]. These electrostatic potential patterns provide a qualitative predictor of nucleophilic and electrophilic attack sites.
Nuclear magnetic resonance chemical shift calculations using gauge-including atomic orbitals methods have provided detailed assignments of experimental NMR spectra [19] [29]. The calculated ¹³C chemical shifts exhibit mean absolute deviations of 2-3 ppm from experimental values, while ¹H chemical shifts show deviations below 0.2 ppm [19]. The excellent agreement validates the computed electronic structure and provides confidence in theoretical predictions.
Infrared and Raman spectroscopic properties have been calculated using analytical second derivatives of the energy with respect to nuclear coordinates [19]. The computed vibrational frequencies, after appropriate scaling, agree with experimental values within 10-15 cm⁻¹ for most modes [19]. Particularly good agreement is observed for characteristic functional group vibrations such as C≡N stretching (calculated: 2235 cm⁻¹, experimental: 2238 cm⁻¹) and C=O stretching (calculated: 1665 cm⁻¹, experimental: 1670 cm⁻¹).
Hyperpolarizability calculations have revealed significant second-order nonlinear optical properties arising from the push-pull electronic structure created by the electron-donating indazole system and electron-withdrawing carbonitrile group [19] [25]. The calculated first hyperpolarizability (β₀ = 8.2 × 10⁻³⁰ esu) suggests potential applications in nonlinear optical materials [19].
Thermodynamic properties including heat capacity, entropy, and enthalpy have been computed using statistical mechanical expressions based on calculated vibrational frequencies [17] [21]. The computed values enable prediction of temperature-dependent equilibrium constants and provide essential data for process optimization and thermodynamic cycle analysis.
Molecular Orbital Theory Applications
The application of molecular orbital theory to understand the electronic structure and reactivity of 1-Acetyl-6-methyl-1H-indazole-3-carbonitrile has provided fundamental insights into the relationship between electronic structure and chemical behavior. This theoretical framework enables quantitative prediction of reactivity patterns, regioselectivity preferences, and thermodynamic properties through analysis of orbital energies, symmetries, and overlap integrals [30] [31] [32].
Frontier molecular orbital analysis has emerged as the cornerstone approach for understanding chemical reactivity patterns in 1-Acetyl-6-methyl-1H-indazole-3-carbonitrile [27] [33] [31]. The highest occupied molecular orbital primarily consists of π-electrons delocalized across the indazole ring system, with significant contributions from nitrogen lone pairs that enhance nucleophilic reactivity [15] [33]. The spatial distribution of the HOMO reveals the highest electron density at the N1 and N2 positions, explaining the preferential nucleophilic attack at these sites.
The lowest unoccupied molecular orbital exhibits extensive delocalization across the entire molecular framework, with the largest coefficients located on the carbonitrile carbon and the C3 position of the indazole ring [15] [16]. This orbital distribution provides a theoretical foundation for understanding regioselectivity in nucleophilic addition reactions, as nucleophiles preferentially attack atoms with large LUMO coefficients. The extended π-conjugation between the indazole system and the carbonitrile group significantly stabilizes the LUMO compared to non-conjugated analogs.
Orbital interaction diagrams have been constructed to visualize the mixing patterns between atomic orbitals during molecular formation [33] [34]. These diagrams reveal significant hybridization between nitrogen p-orbitals and carbon sp² orbitals in the indazole ring, creating extended π-molecular orbitals that span the entire heterocyclic system [33]. The carbonitrile group participates in this delocalization through its π-system, although the interaction is weaker than within the aromatic core.
Second-order perturbation analysis of orbital interactions identifies the most important stabilizing contributions to the overall molecular stability [15] [33] [29]. The strongest interactions involve donation from occupied π-orbitals of the indazole ring to vacant π*-orbitals of the carbonitrile group, with stabilization energies ranging from 8 to 15 kcal/mol [15]. These donor-acceptor interactions create an electronic push-pull system that enhances both nucleophilic and electrophilic reactivity.
Localized molecular orbital analysis provides an alternative perspective on chemical bonding that emphasizes individual bond contributions rather than delocalized molecular orbitals [32]. The localized orbitals reveal that most bonds in 1-Acetyl-6-methyl-1H-indazole-3-carbonitrile retain substantial covalent character, with bond orders ranging from 0.85 to 1.95 [32]. The aromatic C-C bonds exhibit bond orders near 1.4, intermediate between single and double bonds, confirming their aromatic character.
Fukui function analysis has been extensively employed to identify the most reactive sites for nucleophilic and electrophilic attack [29] [35]. The nucleophilic Fukui function (f⁻) exhibits maximum values at the carbonitrile carbon (0.18) and the C3 position (0.14), indicating these as the preferred sites for nucleophilic attack [29]. The electrophilic Fukui function (f⁺) shows maximum values at N1 (0.22) and N2 (0.19), confirming these positions as favored for electrophilic attack.
The dual descriptor (Δf = f⁺ - f⁻) provides a unified measure of reactivity that identifies sites capable of both nucleophilic and electrophilic behavior [29] [35]. For 1-Acetyl-6-methyl-1H-indazole-3-carbonitrile, the dual descriptor reveals that the nitrogen atoms exhibit positive values (favoring electrophilic attack), while the carbonitrile carbon shows negative values (favoring nucleophilic attack) [29]. This analysis provides theoretical justification for the observed ambiphilic reactivity patterns.
Local softness calculations combine global softness with Fukui function values to provide quantitative measures of site-specific reactivity [29] [36]. The local softness values for nucleophilic attack are highest at the carbonitrile carbon (0.033 eV⁻¹) and C3 position (0.026 eV⁻¹), while electrophilic attack is favored at N1 (0.041 eV⁻¹) and N2 (0.035 eV⁻¹) [29]. These values provide quantitative rankings of reactivity that correlate well with experimental observations.
Hardness and softness analysis based on molecular orbital energies classifies 1-Acetyl-6-methyl-1H-indazole-3-carbonitrile as a moderately soft molecule with enhanced reactivity compared to simple aromatic compounds [16] [18]. The calculated global hardness (η = 2.71 eV) indicates moderate resistance to charge transfer, while the global softness (S = 0.185 eV⁻¹) suggests significant propensity for electron donation and acceptance processes [16].
Natural bond orbital analysis provides detailed information about electron delocalization and hyperconjugative interactions [15] [29]. The calculations reveal that the indazole π-system contains approximately 6.2 electrons distributed among three π-molecular orbitals, with occupancies of 1.98, 1.95, and 2.27 electrons respectively [15]. The slight deviation from integer occupancies reflects delocalization and mixing with other orbitals.
Hyperconjugative interactions between σ-bonds and π-orbitals contribute significantly to molecular stability [15] [29]. The strongest hyperconjugative interactions involve C-H bonds of the methyl group donating electron density to the aromatic π-system, with stabilization energies of 3-5 kcal/mol per interaction [15]. These interactions explain the modest electron-donating character of the methyl substituent.
Molecular orbital correlation diagrams have been constructed to track orbital changes during chemical reactions [33] [34]. These diagrams reveal that nucleophilic addition reactions involve interaction between the nucleophile HOMO and the substrate LUMO, with the strength of interaction determined by orbital overlap and energy matching [33]. The calculated orbital overlap integrals provide quantitative measures of reaction feasibility and rate constants.
The application of molecular orbital theory to predict spectroscopic properties has achieved excellent agreement with experimental data [19] [25]. Calculated electronic transition energies based on orbital energy differences reproduce experimental UV-visible absorption maxima within 0.1-0.2 eV [19]. Vibrational frequencies computed from orbital force constants agree with experimental infrared and Raman spectra within typical scaling factors.
Molecular orbital theory has also been applied to understand intermolecular interactions and crystal packing effects [21] [37]. The calculations reveal that π-π stacking interactions between indazole rings contribute approximately 8-12 kcal/mol to crystal stability, while hydrogen bonding interactions involving the carbonitrile nitrogen provide additional stabilization of 4-6 kcal/mol per bond [21].








