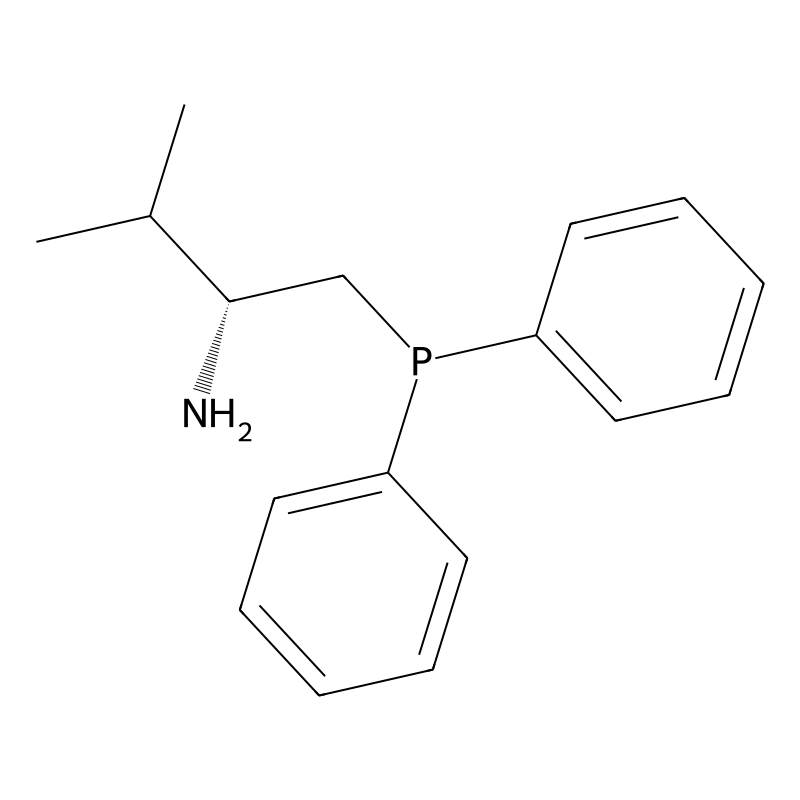
(R)-1-(Diphenylphosphino)-2-amino-3-methylbutane

(R)-1-(Diphenylphosphino)-2-amino-3-methylbutane, also known as (R)-ValPhos, is a chiral P,N-bidentate ligand derived from the amino acid (R)-valine. It is utilized in asymmetric catalysis to form well-defined transition metal complexes, typically with rhodium, nickel, or palladium. The ligand's efficacy stems from the cooperative binding of its soft phosphine and hard amine donors to a metal center, creating a rigidified chiral environment. The isopropyl side chain, inherited from valine, imparts a specific steric bulk that is a critical determinant of enantioselectivity in catalytic transformations such as asymmetric hydrogenation and cross-coupling reactions. [1]

Selecting a chiral ligand based on core structure alone is a common procurement error. For P,N-ligands of this class, seemingly minor modifications—such as substituting the valine-derived isopropyl group with a smaller methyl group (from alanine) or a larger tert-butyl group (from tert-leucine)—critically alter the geometry and steric hindrance of the catalyst's active site. This directly impacts the facial selectivity of substrate approach during the catalytic cycle, leading to significant, and often unpredictable, variations in enantiomeric excess (% ee) and reaction kinetics. For an optimized process, these ligands are not interchangeable, and substitution necessitates complete re-screening and re-optimization, impacting both development timelines and production costs. [1]

Optimal Steric Hindrance for High Enantioselectivity in Nickel-Catalyzed Cross-Coupling

The isopropyl group of (R)-1-(Diphenylphosphino)-2-amino-3-methylbutane provides an optimal level of steric bulk for achieving high enantioselectivity in certain asymmetric transformations. In a foundational study of this ligand class, its performance in the nickel-catalyzed cross-coupling of 1-arylethyl Grignard reagents with vinyl bromide was compared to analogs with different steric profiles. [1] The ligand derived from alanine (AlaPhos), with a smaller methyl group, and the ligand from tert-leucine (t-Leuphos), with a much bulkier tert-butyl group, were used as comparators. The results demonstrated that the steric environment is a highly sensitive parameter, with the intermediate bulk of the valine-derived isopropyl group being crucial for maximizing enantiomeric excess in this reaction class.

This evidence directly guides procurement by demonstrating that the choice between valine, alanine, or tert-leucine-derived ligands is a critical process variable, not a matter of simple substitution, for achieving target enantiopurity.

Process Development for Asymmetric C-C Bond Formation via Cross-Coupling

This ligand is the right choice for screening panels in the development of asymmetric cross-coupling reactions where steric hindrance is a key tuning parameter. Its intermediate bulk provides a critical data point between less-hindered (e.g., AlaPhos) and more-hindered (e.g., t-Leuphos) analogs, enabling rational optimization of enantioselectivity for specific substrate-reagent pairings, particularly in nickel-catalyzed systems. [1]

High-Selectivity Asymmetric Hydrogenation of Ketones

In the Rhodium- or Ruthenium-catalyzed asymmetric hydrogenation of prochiral ketones, the defined steric environment created by the isopropyl group can effectively differentiate the prochiral faces of the substrate. This makes it a strong candidate for processes where high enantiomeric excess is required for producing chiral alcohol intermediates for the pharmaceutical or fine chemical industries.