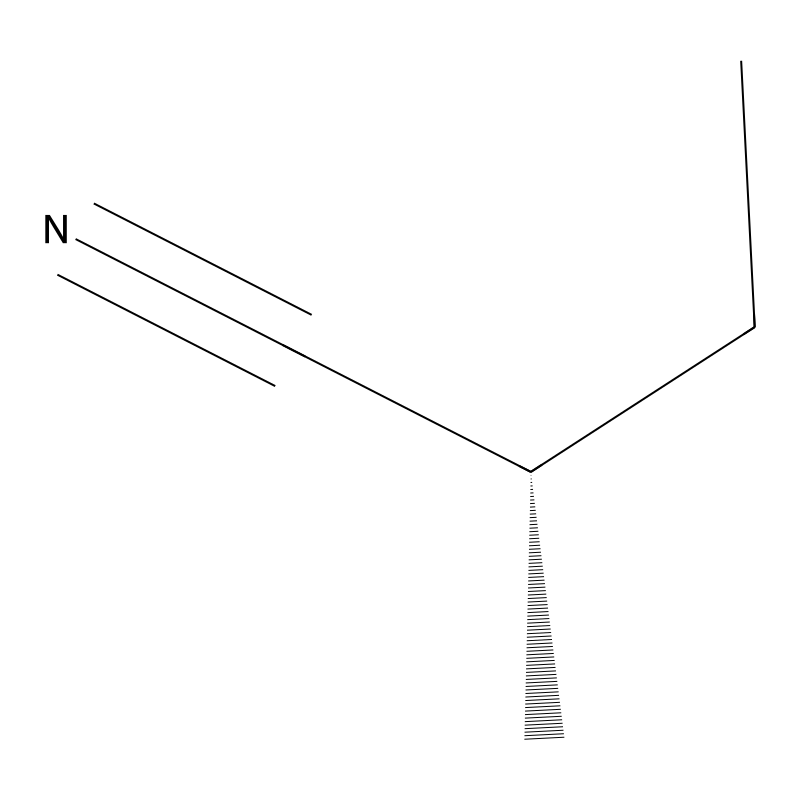
(S)-(+)-2-Methylbutyronitrile
Catalog No.
S3407747
CAS No.
25570-03-0
M.F
C5H9N
M. Wt
83.13 g/mol
Availability
* This item is exclusively intended for research purposes and is not designed for human therapeutic applications or veterinary use.
Content Navigation
CAS Number
25570-03-0
Product Name
(S)-(+)-2-Methylbutyronitrile
IUPAC Name
(2S)-2-methylbutanenitrile
Molecular Formula
C5H9N
Molecular Weight
83.13 g/mol
InChI
InChI=1S/C5H9N/c1-3-5(2)4-6/h5H,3H2,1-2H3/t5-/m0/s1
InChI Key
RCEJCSULJQNRQQ-YFKPBYRVSA-N
SMILES
CCC(C)C#N
Canonical SMILES
CCC(C)C#N
Isomeric SMILES
CC[C@H](C)C#N
Potential Applications in Medicinal Chemistry
One area of research exploring (S)-(+)-2-Methylbutyronitrile is its potential as a building block for drug development. Its chiral structure allows for the creation of enantiopure drugs, which can offer several advantages over racemic mixtures (mixtures of both enantiomers) in terms of efficacy and safety []. Studies have investigated its use in the synthesis of various drug candidates, including anticonvulsants and antidepressants [, ].
XLogP3
1.1
GHS Hazard Statements
Aggregated GHS information provided by 38 companies from 1 notifications to the ECHA C&L Inventory. Each notification may be associated with multiple companies.;
H226 (100%): Flammable liquid and vapor [Warning Flammable liquids];
H302 (100%): Harmful if swallowed [Warning Acute toxicity, oral];
H312 (100%): Harmful in contact with skin [Warning Acute toxicity, dermal];
H332 (100%): Harmful if inhaled [Warning Acute toxicity, inhalation];
Information may vary between notifications depending on impurities, additives, and other factors. The percentage value in parenthesis indicates the notified classification ratio from companies that provide hazard codes. Only hazard codes with percentage values above 10% are shown.
H226 (100%): Flammable liquid and vapor [Warning Flammable liquids];
H302 (100%): Harmful if swallowed [Warning Acute toxicity, oral];
H312 (100%): Harmful in contact with skin [Warning Acute toxicity, dermal];
H332 (100%): Harmful if inhaled [Warning Acute toxicity, inhalation];
Information may vary between notifications depending on impurities, additives, and other factors. The percentage value in parenthesis indicates the notified classification ratio from companies that provide hazard codes. Only hazard codes with percentage values above 10% are shown.
Pictograms
Flammable;Irritant
Wikipedia
(2S)-2-methylbutanenitrile
Dates
Modify: 2023-08-19
Explore Compound Types
Get ideal chemicals from 750K+ compounds
CAS No.:6915-57-7
Molecular Formula:C6H2BiBr4O3
Molecular Weight:649.67 g/mol
Availability:
In Stock
CAS No.:1986-70-5
Molecular Formula:C29H40O9
Molecular Weight:532.6 g/mol
Availability:
Inquiry
CAS No.:1004-29-1
Molecular Formula:C8H16O
Molecular Weight:128.21 g/mol
Availability:
In Stock
CAS No.:13091-93-5
Molecular Formula:C15H25N6O7PS
Molecular Weight:464.4 g/mol
Availability:
In Stock
CAS No.:38216-54-5
Molecular Formula:C15H10O6
Molecular Weight:286.24 g/mol
Availability:
In Stock
CAS No.:13966-05-7
Molecular Formula:Ca
Molecular Weight:44.956186 g/mol
Availability:
In Stock
CAS No.:110726-28-8
Molecular Formula:C29H28O3
Molecular Weight:424.5 g/mol
Availability:
In Stock
CAS No.:65929-03-5
Molecular Formula:C22H33N3O5S
Molecular Weight:451.6 g/mol
Availability:
In Stock
CAS No.:81017-02-9
Molecular Formula:C10H14O3
Molecular Weight:182.22 g/mol
Availability:
In Stock
