Nitrobenzene
Content Navigation
CAS Number
Product Name
IUPAC Name
Molecular Formula
Molecular Weight
InChI
InChI Key
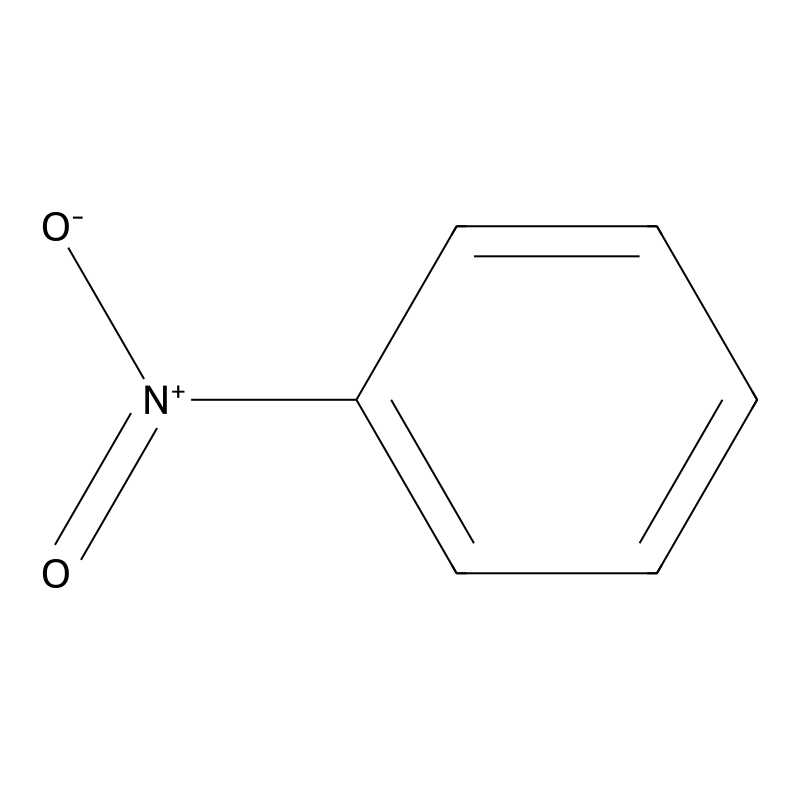
SMILES
solubility
0.02 M
Slightly soluble in carbon tetrachloride; very soluble in ethanol, diethyl ether, acetone, benzene
Soluble in ~500 parts water; freely soluble in alcohol, benzene, ether, oils
Readily soluble in most organic solvents and is completely miscible with diethyl ether, benzene, and alcohol.
Slightly soluble in water with a solublity of 0.19% at 20 °C and 0.8% at 80 °C
In water, 2.09X10+3 mg/L at 25 °C
2.09 mg/mL at 25 °C
Solubility in water, g/100ml: 0.2
0.2%
Synonyms
Canonical SMILES
Nitrobenzene (CAS 98-95-3) is the simplest aromatic nitro compound, consisting of a benzene ring substituted with a single nitro group. It serves as a critical, large-scale industrial precursor, with approximately 95-97% of its production dedicated to the synthesis of aniline, a key intermediate for polyurethanes, rubber chemicals, dyes, and pharmaceuticals. Beyond its primary role as a chemical intermediate, nitrobenzene is also utilized as a specialized polar solvent in certain applications, such as in petroleum refining and for cellulose ether manufacturing, and as a benchmark material in electro-optics due to its significant Kerr effect. Its well-defined physical properties and established reactivity profile make it a fundamental building block in organic synthesis.
Procurement Fit
References
- [2] Nitrobenzene: general information. GOV.UK.
- [3] Booth, G. (2000). Nitro Compounds, Aromatic. In Ullmann's Encyclopedia of Industrial Chemistry. Wiley-VCH Verlag GmbH & Co. KGaA.
- [4] Toxicological Profile for Nitrobenzene. Agency for Toxic Substances and Disease Registry (ATSDR).
- [5] IARC Working Group on the Evaluation of Carcinogenic Risks to Humans. (1996). Printing Processes and Printing Inks, Carbon Black and Some Nitro Compounds. In IARC Monographs on the Evaluation of Carcinogenic Risks to Humans (No. 65). International Agency for Research on Cancer.
- [6] Kerr effect. Wikipedia.
- [7] Nitrobenzene. Wikipedia.
Substituting nitrobenzene with structurally similar compounds like nitrotoluenes or dinitrobenzenes is fundamentally unviable for its primary application: the production of unsubstituted aniline. The introduction of any additional substituent, such as a methyl group in nitrotoluene, directly alters the final product to a substituted aniline (e.g., toluidine), which has entirely different industrial applications and physical properties. Furthermore, physical and processability differences prevent direct substitution. For instance, dinitrobenzenes are solids at room temperature, unlike liquid nitrobenzene, requiring different handling and reactor feeding systems. More critically, increasing the degree of nitration (e.g., to dinitrobenzene) significantly alters thermal stability and reactivity, introducing different process safety risks and demanding distinct reaction conditions that are incompatible with processes optimized for nitrobenzene.
Substitution Risk
References
- [1] Vogel, A. I., Furniss, B. S., Hannaford, A. J., Smith, P. W. G., & Tatchell, A. R. (1989). Vogel's Textbook of Practical Organic Chemistry (5th ed.). Longman Scientific & Technical.
- [2] Chen, J. R., Tsai, Y. T., & Shu, C. M. (2011). Thermal hazard assessment of nitrobenzene/dinitrobenzene mixtures. Journal of hazardous materials, 188(1-3), 52–57.
- [3] Bazarov, D. V., et al. (2012). Investigation of thermal stability of some nitroaromatic derivatives by DSC. Journal of Thermal Analysis and Calorimetry, 110(1), 147-151.
High-Yield Aniline Precursor
Nitrobenzene is the direct and indispensable precursor for industrial aniline synthesis, with processes optimized to achieve near-quantitative conversion. Industrial-scale catalytic hydrogenation processes are designed specifically for nitrobenzene, targeting aniline yields of 97% or higher under optimized conditions. Substitution with analogs like p-nitrotoluene, while also reducible, yields p-toluidine, a completely different chemical product. The kinetics and selectivity of the hydrogenation are highly dependent on the unsubstituted phenyl core; the presence of other functional groups requires significant process re-optimization and can introduce alternative reaction pathways or catalyst poisoning effects, making nitrobenzene the specific choice for aniline production.
| Evidence Dimension | Product Specificity in Catalytic Hydrogenation |
| Target Compound Data | Yields aniline with >97% selectivity in optimized industrial processes. |
| Comparator Or Baseline | Substituted nitroaromatics (e.g., nitrotoluenes, nitrophenols) yield corresponding substituted anilines (toluidines, aminophenols), not aniline. |
| Quantified Difference | Qualitative but absolute: The end product is fundamentally determined by the precursor's structure. |
| Conditions | Industrial-scale heterogeneously catalyzed hydrogenation (e.g., Pd/Al2O3 catalyst, elevated temperature and pressure). |
For the production of aniline, the largest use case, there is no direct substitute for nitrobenzene; any structural change in the precursor alters the final product.
Electrochemical Reduction Standard
Nitrobenzene exhibits a well-characterized electrochemical reduction potential, making it a standard reference compound. At pH 7, the half-wave potential (E1/2) for the reduction of nitrobenzene to phenylhydroxylamine occurs in the range of -0.30 to -0.45 V vs. SCE. This value is distinct from substituted nitroaromatics; for example, the reduction potentials of nitrotoluenes are shifted due to the electron-donating effect of the methyl group, making them slightly harder to reduce. This defined potential is critical for applications in electrosynthesis, where precise voltage control is necessary to achieve selective reduction without side reactions, and in analytical methods where it serves as a reliable calibrant.
| Evidence Dimension | Half-Wave Reduction Potential (E1/2) vs. SCE at pH 7 |
| Target Compound Data | -0.30 to -0.45 V |
| Comparator Or Baseline | Substituted nitroaromatics (e.g., nitrotoluenes) exhibit different reduction potentials due to electronic effects of substituents. |
| Quantified Difference | The specific potential window allows for selective electrochemical transformations not directly applicable to its analogs without recalibration. |
| Conditions | Aqueous medium, pH 7, vs. Saturated Calomel Electrode (SCE). |
This specific and well-documented reduction potential allows for precise process control in electrosynthesis and makes it a reliable standard in electrochemical research, a role its analogs cannot fill without characterization.
Kerr Effect Benchmark
Nitrobenzene possesses one of the highest known Kerr constants among common liquids, establishing it as the benchmark material for Kerr cells used in high-speed light modulation and electro-optical shutters. Its Kerr constant (K) is approximately 4.4 × 10⁻¹² m·V⁻², which is orders of magnitude greater than many other solvents. For comparison, the Kerr constant for water is ~9.4 × 10⁻¹⁴ m·V⁻², and for less polar aromatic compounds like benzene or toluene, the effect is significantly smaller. While some highly specialized, multi-ring aromatic compounds can exhibit higher constants, they often suffer from poor solubility or stability, making pure, liquid nitrobenzene the most practical and widely-cited standard for high-performance applications.
| Evidence Dimension | Kerr Constant (K) |
| Target Compound Data | 4.4 × 10⁻¹² m·V⁻² |
| Comparator Or Baseline | Water: 9.4 × 10⁻¹⁴ m·V⁻² |
| Quantified Difference | Nitrobenzene's Kerr constant is approximately 47 times greater than that of water. |
| Conditions | Standard conditions, visible light wavelength. |
For applications requiring a strong, fast, and reliable electro-optical response, nitrobenzene's exceptionally high Kerr constant makes it the material of choice over common solvents or simpler aromatics.
Thermal Hazard Comparison
While all nitroaromatic compounds are energetic, nitrobenzene exhibits a more manageable thermal hazard profile compared to its polynitrated counterparts like dinitrobenzene (DNB). Differential Scanning Calorimetry (DSC) shows that the onset of exothermic activity for pure nitrobenzene begins around 300 °C. In contrast, mixtures containing DNB, or DNB itself, can exhibit lower thermal stability, with exotherms beginning at significantly lower temperatures (e.g., in the 263-280 °C range for certain mixtures). This higher decomposition temperature for the monosubstituted nitrobenzene provides a wider and safer operating window for high-temperature processes, such as vapor-phase hydrogenations, a critical consideration for industrial procurement and process design.
| Evidence Dimension | Onset Temperature of Exothermic Decomposition (ARC) |
| Target Compound Data | Decomposition onset for pure nitrobenzene is above the 263-280 °C range. |
| Comparator Or Baseline | Nitrobenzene/Dinitrobenzene mixtures: Onset of exotherm begins in the 263-280 °C range. |
| Quantified Difference | Pure nitrobenzene is more thermally stable than mixtures containing its dinitrated byproduct, offering a tangible safety margin. |
| Conditions | Accelerating Rate Calorimetry (ARC) experiments. |
Choosing nitrobenzene over polynitrated aromatics provides a critical process safety advantage due to its higher thermal stability, reducing the risk of runaway reactions.
Industrial Aniline Production
Nitrobenzene is the sole industrial starting material for the production of unsubstituted aniline. Its use in optimized, large-scale catalytic hydrogenation processes allows for aniline yields exceeding 97%, a benchmark that cannot be met by using substituted analogs which would result in different products.
Electro-Optical Kerr Cell Medium
Due to its exceptionally large and well-documented Kerr constant, nitrobenzene is the preferred liquid medium for constructing Kerr cells. These devices are used for high-speed light modulation, Q-switching in lasers, and as calibration standards in nonlinear optical research, where weaker-responding solvents are inadequate.
Electrosynthesis of Aniline
The well-defined reduction potential of nitrobenzene allows for precise electrochemical conversion to aniline or intermediate products like phenylhydroxylamine. This makes it a model substrate for developing and optimizing electrosynthetic routes that require high selectivity and avoidance of harsh chemical reductants.
Nitroaromatic Model Compound
As the simplest nitroaromatic compound, nitrobenzene serves as a crucial reference in studies of catalytic reduction mechanisms, bioremediation pathways, and toxicological assessments. Its predictable thermal and chemical behavior, compared to more complex or polynitrated analogs, provides a reliable baseline for comparative studies.
Application Fit
References
- [1] Koprivova, H., et al. (2021). Toward High Selectivity Aniline Synthesis Catalysis at Elevated Temperatures. Industrial & Engineering Chemistry Research, 60(13), 4785-4795.
- [2] Kerr effect. Wikipedia.
- [3] Misra, A., Kumar, A., & Pandey, P. C. (2015). Single- and Two-Electron Reduction of Nitroaromatic Compounds by Flavoenzymes: Mechanisms and Implications for Cytotoxicity. In Free Radicals in Human Health and Disease (pp. 227-253). Springer, New Delhi.
- [4] Ju, K. S., & Parales, R. E. (2010). Nitroaromatic compounds, from synthesis to biodegradation. Microbiology and molecular biology reviews, 74(2), 250–272.
- [5] Chen, J. R., Tsai, Y. T., & Shu, C. M. (2011). Thermal hazard assessment of nitrobenzene/dinitrobenzene mixtures. Journal of hazardous materials, 188(1-3), 52–57.
Physical Description
Liquid
PALE YELLOW OILY LIQUID WITH CHARACTERISTIC ODOUR.
Yellow to dark brown, oily liquid with a pungent odor like paste shoe polish.
Yellow, oily liquid with a pungent odor like paste shoe polish. [Note: A solid below 42°F.]
Color/Form
Colorless to yellow, oily liquid (Note: A solid below 42 degrees F).
Bright-yellow crystals or pale-yellow to colorless, oily liquid
XLogP3
Boiling Point
210.8 °C
211 °C
411°F
Flash Point
190 °F (88 °C) (Closed cup)
88 °C c.c.
190°F
Vapor Density
4.25 (Air = 1)
Relative vapor density (air = 1): 4.2
4.3
Density
1.2037 g/cu cm at 20 °C
Relative density (water = 1): 1.2
1.20
LogP
log Kow = 1.85
1.85
1.86
Odor
Pungent odor like paste shoe polish
Melting Point
5.7 °C
5.7°C
5 °C
42°F
UNII
GHS Hazard Statements
H311: Toxic in contact with skin [Danger Acute toxicity, dermal];
H331: Toxic if inhaled [Danger Acute toxicity, inhalation];
H351: Suspected of causing cancer [Warning Carcinogenicity];
H360F: May damage fertility [Danger Reproductive toxicity];
H372: Causes damage to organs through prolonged or repeated exposure [Danger Specific target organ toxicity, repeated exposure];
H412: Harmful to aquatic life with long lasting effects [Hazardous to the aquatic environment, long-term hazard]
Pharmacology
Mechanism of Action
The particular redox chemistry associated with nitrobenzene metabolism in red blood cells (RBCs) is of special interest because of its association with the development of methemoglobinemia. ...An association of metHb formation with the reduction of nitrobenzene to nitrosobenzene, phenylhydroxylamine, and aniline by nitroreductases present within intestinal microflora /has been observed/. Moreover, in vitro incubation of RBCs with nitrobenzene does not result in the formation of metHb. Taken together, these findings suggest that it is the presence and cycling of the reductive products of nitrobenzene within RBCs that cause the conversion of oxyhemoglobin (oxyHb) to metHb. ... The primary metabolic event in the formation of metHb (Fe3+) from oxyHb (Fe2+) as a result of nitrobenzene exposure is the cycling between phenylhydroxylamine and nitrosobenzene.
In acute ... and subchronic studies in rodents ..., lesions in the brain stem and cerebellum were the most life-threatening toxic effects seen. In severe methemoglobinemia arising from extensive nitrobenzene poisoning, central nervous system effects may be predicted on the basis of hypoxia alone. It has also been hypothesized that these lesions might represent a hepatic encephalopathy secondary to the liver toxicity of nitrobenzene ... Other results suggest that it is possible that brain parenchymal damage may have resulted from anoxia or hypoxia due to vascular damage or decreased blood flow to affected areas ... Another possible mechanism for the central nervous system damage is the formation of superoxide radicals or toxic hydroxyl radicals generated from hydrogen peroxide ... Evidence has been adduced to indicate that the ability of a related compound, dinitrobenzene, to cause cell death in in vitro co-cultures of rat brain astrocytes and brain capillary endothelial cells (a blood-brain barrier model) is at least partly due to the generation of hydroxyl radicals in the culture.
... Cecal contents obtained and incubated in an anaerobic environment are capable of reducing nitrobenzene. Incubation of radioactive nitrobenzene with isolated rat hepatocytes under aerobic conditions produces no metabolites detectable by counting fractions of eluate from a high pressure liquid chromatographic system and no measurable disappearance of the parent compound. ... Conventional rats excrete an oral dose of nitrobenzene in the urine as an unknown metabolite, p-hydroxyacetanilide-sulfate, p-nitrophenol-sulfate, and m-nitrophenol-sulfate. /It was/ concluded that it is clear that metabolism by both mammalian and bacterial enzyme systems is important to the expression of toxicity of nitroaromatic compounds.
Exposure of rats to nitrobenzene produces a degeneration of the seminiferous epithelium of the testes. Sperm production was continuously monitored in rats surgically prepared by anastomosing the vas deferentia with the urinary bladder to evaluate the reversibility of nitrobenzene toxicity. Rates of sperm production were monitored by collecting urine and counting sperm microscopically with hemocytometer. Six weeks after surgery, rats were dosed po with a single dose of 300 mg/kg of nitrobenzene in corn oil. Sperm were not detected in the urine of treated rats between 32 and 48 days after treatment. Despite the fact that degenerative changes in the siminiferous tubules were observed histologically as early as 3 days after dosing, there was a 32-day lag period between treatment and cessation of sperm output in treated rats. Histological examination showed that pachytene spermatocytes and step 1-2 spermatides were the most susceptible cell stages to nitrobenzene and were observed forming into giant cells as early as 3 days after treatment. However, repair was substantial by 3 weeks after treatment and by days 76-100, the rate of sperm output reached 78% of the control group. By 100 days after treatment, there was greater than 90% regeneration of the seminiferous epithelium. Thus, a single oral dose of nitrobenzene induced testicular degeneration and approximately a 17-day period of aspermia resulted. Back-dating of the aspermic period to the timing of the spermatogenic cycle closely corresponded with the same germ cell stages that were observed degenerating in histologic examinations. Thus, changes in sperm output from vasocystotomized rats correlated well with histopathologic changes, demonstrating the value of this technique for toxicity studies.
The equilibrium binding of nitrobenzene to plasma proteins /were studied/ in vitro in pooled plasma samples from Sprague Dawley rats (sex unspecified). Aliquots of pooled plasma samples spiked with 0.32-933 mg/l nitrobenzene were allowed to equilibrate for 30-90 min at 25 °C. Of the nitrobenzene, 72.0 + or - 4.5% were bound to the rat plasma proteins.
Vapor Pressure
0.25 mmHg
0.245 mm Hg at 25 °C (est)
Vapor pressure, Pa at 20 °C: 20
0.3 mmHg at 77°F
(77°F): 0.3 mmHg
Pictograms
Acute Toxic;Health Hazard
Impurities
Other CAS
26969-40-4
4165-60-0
Wikipedia
Biological Half Life
(14)C-Nitrobenzene /was injected/ intravenously into volunteers. Excretion in the urine was 60.5% of the dose over five days. The elimination half-life was 20 hours.
Measurement of nitrobenzene concn in blood of an acutely exposed person indicated that the cmpd is cumulative ... /and remains/ in human body for a prolonged period. There have been similar observations of persistence of 2 major urinary metabolites, p-aminophenol and p-nitrophenol, in patient streated for acute or subacute poisoning. Because of slow rate of nitrobenzene metabolism in humans, concn of p-nitrophenol in urine incr for approx 4 days during exposure, eventually reaching a value 2.5 times that found during the first day. Half-life for urinary excretion of p-nitrophenol from humans after single dose was approx 60 hr; 84 hr was observed in female who attempted suicide ... Urinary metabolites in humans account for only 20% or 30% of nitrobenzene dose.
Use Classification
Hazardous Air Pollutants (HAPs)
Fire Hazards -> Carcinogens, Teratogens, Flammable - 2nd degree, Reactive - 1st degree
Methods of Manufacturing
From benzene by nitrating with nitric acid-sulfuric acid mix.
CHEMICAL PROFILE: Nitrobenzene. /Nitrobenzene is/ produced by the nitration of benzene using a mixture of nitric acid and sulfuric acid.
General Manufacturing Information
All other basic organic chemical manufacturing
Petrochemical manufacturing
Pharmaceutical and medicine manufacturing
Printing ink manufacturing
Synthetic dye and pigment manufacturing
Benzene, nitro-: ACTIVE
Method of purification: By washing and distilling with steam then redistilling.
Analytic Laboratory Methods
EPA Method 8250. Packed Column Gas Chromatography/Mass Spectrometry Technique for the determination of semivolatile organic compounds in extracts prepared from all types of solid waste matrices, soil, and groundwater. This method is applicable to quantify most neutral, acidic, and basic organic compounds that are soluble in methylene chloride and capable of being eluted wtih derivatization as sharp peaks from a gas chromatographic packed column. Under the prescribed conditions, nitrobenzene has a detection limit of 1.9 ug/l. Precision and method accuracy were found to be directly related to the concentration of the analyte and essentially independent of the sample matrix.
EPA Method 8270. Capillary Column Gas Chromatography/Mass Spectrophotometry. This method is used for the determination of semivolatile organic compounds in extracts prepared from all types of solid waste matrices, soils, and groundwater. This method is applicable to quantify most acidic, basic, and neutral organic compounds that are soluble in methylene chloride and are capable of being eluted without derivatization as sharp peaks from a capillary column (DB-5 or equivalent). The Practical Quantitation Limit for nitrobenzene is 10 ug/l in ground water and 660 ug/kg in low soil/sediment. The precision and a method accuracy were found to be directly related to the concentration of the analyte and essentially independent of the sample matrix.
Method: NIOSH 2005, Issue 3; Procedure: gas chromatography with flame ionization detector; Analyte: nitrobenzene; Matrix: air; Detection Limit: 0.6 ug/sample.
For more Analytic Laboratory Methods (Complete) data for NITROBENZENE (25 total), please visit the HSDB record page.
Clinical Laboratory Methods
Storage Conditions
PRECAUTIONS FOR "CARCINOGENS": Storage site should be as close as practical to lab in which carcinogens are to be used, so that only small quantities required for ... expt need to be carried. Carcinogens should be kept in only one section of cupboard, an explosion-proof refrigerator or freezer (depending on chemicophysical properties ...) that bears appropriate label. An inventory ... should be kept, showing quantity of carcinogen & date it was acquired ... Facilities for dispensing ... should be contiguous to storage area. /Chemical Carcinogens/
Interactions
Synergism between orally administered nitrobenzene and six other common industrial compounds (formalin, butylether, aniline, dioxane, acetone, and carbon tetrachloride) was demonstrated in rat studies using death as the end-point.
When alcohol was given orally and nitrobenzene was given intravenously, there was increased toxicity in rabbits. Alcohol also enhanced the neural toxicity of nitrobenzene in rabbits when nitrobenzene was applied to the skin.
To determine whether nitro reduction by the gut flora can play an important role in chem toxicity, methemoglobin formation was measured after admin of nitrobenzene to germ-free rats and to germ-free rats acclimatized to the normal animal room. When nitrobenzene (200 mg/kg in sesame oil) was admin to normal male Sprague Dawley rats ip, about 30-40% of blood hemoglobin was converted to methemoglobin within 1-2 hr. When same dose was given to germ-free or antibiotic pretreated rats, no measurable methemoglobin formation occurred even up to 7 hr after admin. Since germ-free animals are free from microbial flora, gut flora present in normal and acclimatized animals may be responsible for redn of nitrobenzene in vivo and subsequent methemoglobin formation.
Westerhaus et al. Heterogenized cobalt oxide catalysts for nitroarene reduction by pyrolysis of molecularly defined complexes. Nature Chemistry, doi: 10.1038/nchem.1645, published online 12 May 2013 http://www.nature.com/nchem
Explore Compound Types
