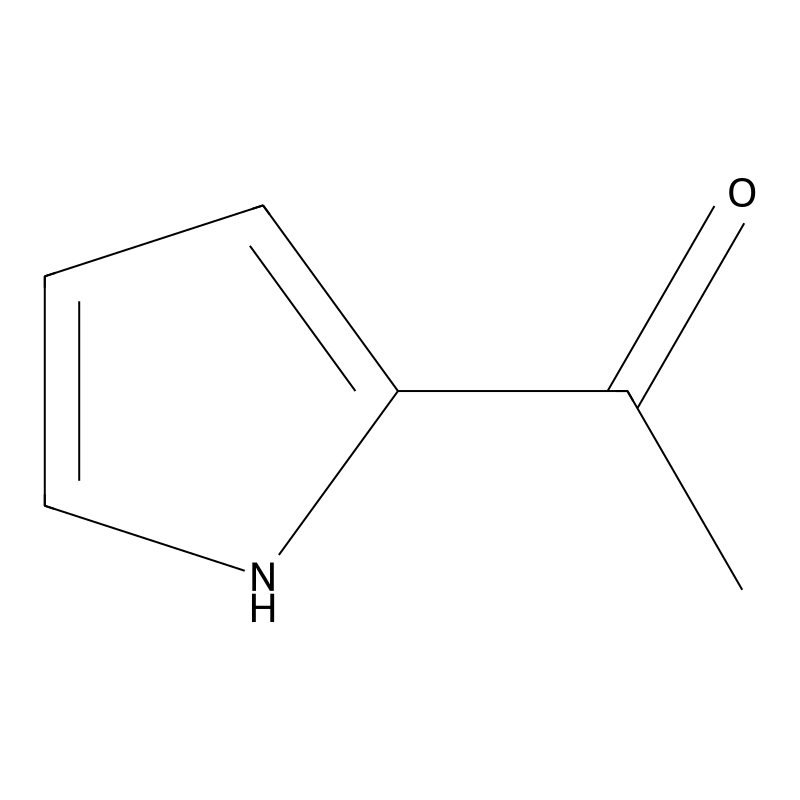
2-Acetylpyrrole

2-Acetylpyrrole is a key heterocyclic ketone, distinguished by a five-membered aromatic pyrrole ring functionalized with an acetyl group at the C2 position. This specific substitution pattern makes it a critical precursor in the synthesis of more complex organic molecules, including pharmaceuticals, porphyrins, and other bioactive compounds. Its utility stems from the acetyl group's ability to direct further reactions and serve as a handle for chain extension, while the pyrrole core provides a foundational structure for numerous important chemical classes. Unlike unsubstituted pyrrole, the acetyl group modifies the ring's reactivity in a predictable manner, enabling its use in controlled, multi-step synthetic pathways.

Substituting 2-acetylpyrrole with seemingly similar compounds like 2-acetylfuran or unsubstituted pyrrole often leads to process failure or suboptimal outcomes. The nitrogen heteroatom in 2-acetylpyrrole provides a crucial N-H group for hydrogen bonding and serves as a site for N-alkylation, properties entirely absent in 2-acetylfuran. This difference is critical in syntheses where intermolecular interactions or subsequent N-functionalization are required. Compared to unsubstituted pyrrole, the C2-acetyl group is strongly electron-withdrawing, which deactivates the ring to uncontrolled electrophilic polymerization and allows for predictable, regioselective substitution at other positions. Using unsubstituted pyrrole can result in lower yields and a mixture of isomers, complicating purification and reducing process efficiency. Therefore, for syntheses requiring controlled reactivity and specific hydrogen-bonding capabilities, 2-acetylpyrrole is the necessary, non-interchangeable starting material.

Increased Oxidation Potential for Controlled Electropolymerization Compared to Unsubstituted Pyrrole

The electron-withdrawing acetyl group at the C2 position significantly increases the oxidation potential of 2-acetylpyrrole compared to the unsubstituted pyrrole monomer. The oxidation potential of pyrrole is approximately +0.7 to +0.8 V, while its resulting polymer has a lower oxidation potential near -0.2 V. This high initial oxidation potential for the monomer makes polymerization difficult to control and prone to over-oxidation. The acetyl group on 2-acetylpyrrole raises this initial monomer oxidation potential, allowing for more controlled electrochemical polymerization and the formation of functionalized polymers with tailored electronic properties not achievable with the basic pyrrole monomer.

For researchers developing functional conducting polymers, this higher oxidation potential allows for greater control over polymerization, preventing unwanted side reactions and enabling the synthesis of more defined materials.

Enables Regioselective Acylation, Avoiding Isomeric Mixtures Seen with Unsubstituted Pyrrole

The C2-acetyl group acts as a powerful directing group in electrophilic substitution reactions. Friedel-Crafts acylation of 2-acetylpyrrole with acetic acid-trifluoroacetic anhydride yields the 2,4-diacetylpyrrole derivative with 46% yield and the 2,5-diacetyl derivative with 19% yield. In contrast, similar reactions with unsubstituted pyrrole often lead to complex mixtures of poly-acylated and polymerized products that are difficult to separate. The deactivating effect of the acetyl group prevents over-reaction and directs incoming electrophiles primarily to the C4 and C5 positions, providing a predictable route to specific isomers that is not feasible with the more reactive, unsubstituted pyrrole.

This predictable reactivity is critical for procurement in multi-step pharmaceutical or fine chemical synthesis, as it ensures higher yields of the desired isomer, simplifies purification, and reduces waste.

Critical Precursor for Bioactive Natural Product Analogs like Prodigiosin

2-Acetylpyrrole is a key building block for the synthesis of prodigiosin analogs, a class of tripyrrolic red pigments with notable antibacterial, antifungal, and anticancer activities. Synthetic routes to these complex molecules often rely on the condensation of a bipyrrolic aldehyde with a functionalized monopyrrole. 2-Acetylpyrrole serves as an essential starting material for creating the required monopyrrole fragment, where the acetyl group is transformed into other functionalities necessary for the final coupling step. Direct substitution with other heterocyclic ketones like 2-acetylfuran would not produce the required nitrogen-containing core structure essential for the prodigiosin scaffold.

For chemists in natural product synthesis and drug discovery, 2-acetylpyrrole is a non-negotiable precursor for accessing the prodigiosin family of compounds, making it a critical procurement choice for this research area.

Synthesis of Regiochemically Defined Pharmaceutical Intermediates

Leveraging its role as a directing group, 2-acetylpyrrole is the ideal choice for syntheses requiring predictable and selective functionalization of the pyrrole ring, such as the preparation of 2,4-disubstituted pyrroles. This ensures higher yields and purities of the target molecule, a critical factor in pharmaceutical development workflows.

Development of Functional Conducting Polymers with Controlled Properties

The modified electronic properties of 2-acetylpyrrole make it a superior monomer choice over unsubstituted pyrrole for creating specialized conducting polymers. Its higher oxidation potential allows for more controlled electropolymerization, leading to materials with tailored conductivity and stability for applications in sensors or electronic devices.

Precursor for Bioactive Natural Products and Analogs

As an indispensable building block for complex natural products like prodigiosin, 2-acetylpyrrole is the go-to material for research groups in medicinal chemistry and chemical biology aiming to synthesize and study this class of potent bioactive agents. Its unique structure is essential for constructing the core scaffold of these molecules.