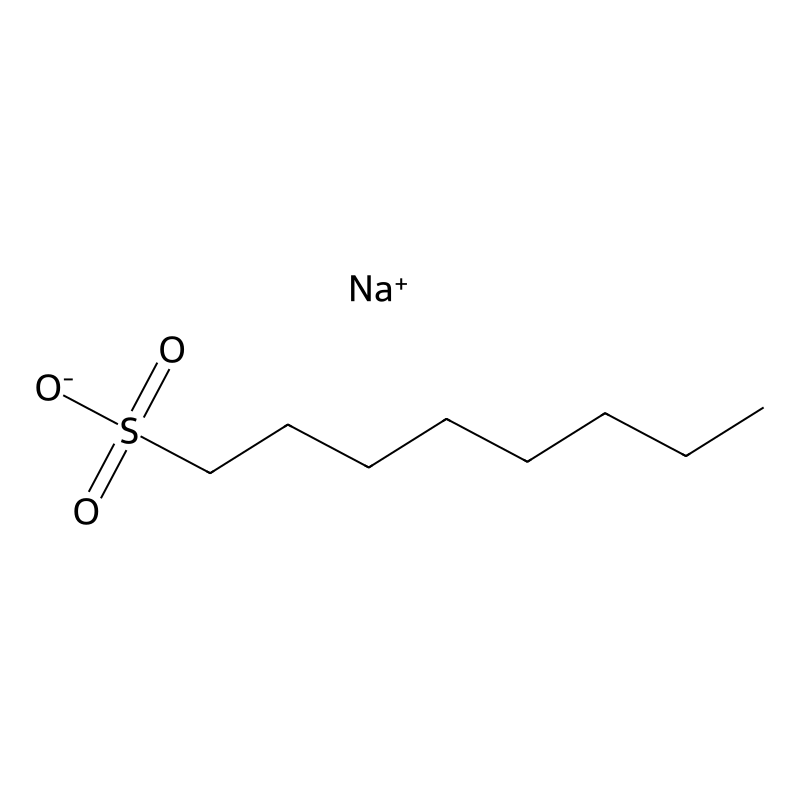
Sodium 1-octanesulfonate

High-Performance Liquid Chromatography (HPLC):

• Ion pairing agent: It acts as an ion pairing agent, especially for separating peptides and proteins in HPLC analysis. These agents help improve peak separation and resolution by altering the charge and hydrophobicity of analytes, resulting in better detection and quantification [].

Surface-active agent:

• Micellar solubilization: Due to its amphiphilic nature, Sodium 1-octanesulfonate can act as a surface-active agent, forming micelles in aqueous solutions. These micelles can solubilize hydrophobic molecules, aiding in their study and analysis [].

Other Applications:

• Interaction with biomolecules: Research suggests that Sodium 1-octanesulfonate can interact with biomolecules like human serum albumin (HSA), potentially impacting its structure and function []. Further studies are needed to understand the implications of this interaction.

Environmental and safety considerations:

• Safer Choice designation: The US Environmental Protection Agency (EPA) has designated Sodium 1-octanesulfonate as a Safer Choice chemical, indicating its lower potential for environmental and human health hazards compared to other alternatives [].

NaOS is an ionic compound, consisting of a sodium cation (Na+) and a 1-octanesulfonate anion (CH3(CH2)6CH2SO3-). It's a white, crystalline solid readily soluble in water []. Its significance lies in its ability to modify the behavior of other molecules during analysis, making them more readily detectable or separable [].

Molecular Structure Analysis

The key feature of NaOS's structure is the octane chain (eight carbon atoms) attached to a sulfonate group (SO3-). The sulfonate group is negatively charged, while the octane chain is hydrophobic (water-fearing). This combination allows NaOS to interact with both water and organic molecules [].

Chemical Reactions Analysis

NaOS doesn't readily undergo complex chemical reactions. However, its primary application lies in ion-pairing. Here, NaOS interacts with ionic or charged organic molecules, forming neutral ion pairs. This changes the molecules' solubility and chromatographic behavior, allowing for better separation during techniques like High-Performance Liquid Chromatography (HPLC) [, ].

For instance, a study used NaOS as an ion-pairing agent for HPLC analysis of paraquat (methyl viologen) in tissues []. The ion pair formed between NaOS and paraquat improved its retention time on the HPLC column, allowing for easier detection.

Physical And Chemical Properties Analysis

• Melting Point: ≥ 300 °C (lit.) [].
• Boiling Point: Decomposes before boiling [].
• Solubility: Highly soluble in water (clear, colorless solution) [, ].
• Stability: Stable under normal temperatures [].

In ion-pairing, the negatively charged sulfonate group of NaOS interacts with positively charged molecules, forming a neutral ion pair. This alters the molecule's polarity and affinity for the mobile and stationary phases in chromatography techniques like HPLC. This can improve separation and detection of specific molecules [].