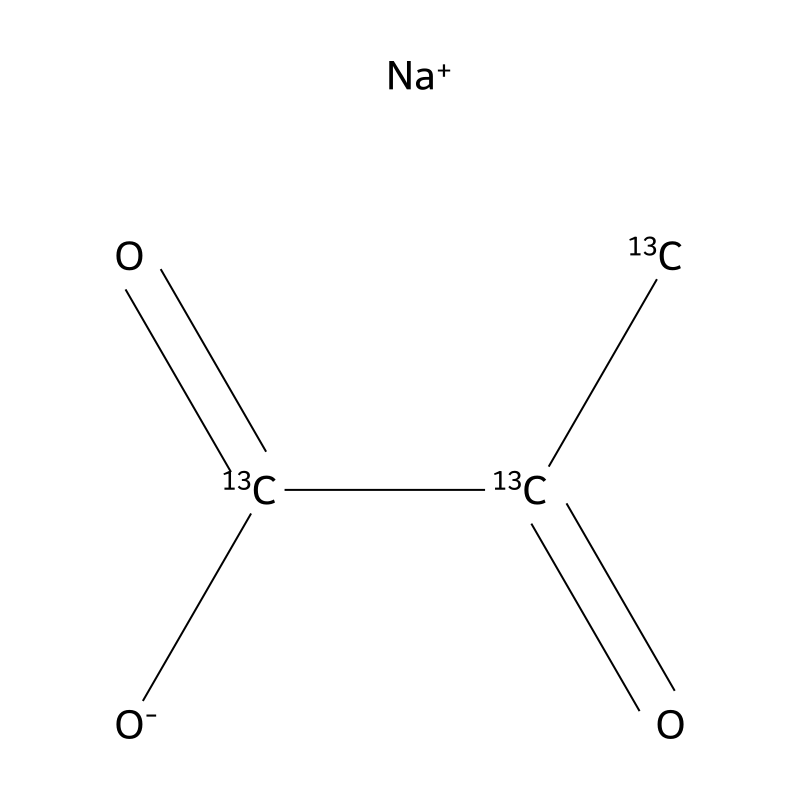
sodium;2-oxo(1,2,3-13C3)propanoate

Studying Brain Metabolism of Exogenous Pyruvate

One crucial application of Sodium pyruvate-(13-C)3 involves investigating the brain's ability to utilize externally introduced pyruvate (exogenous pyruvate) as an energy source []. Researchers administer this compound and then use techniques like nuclear magnetic resonance (NMR) spectroscopy to track the metabolic fate of the labeled carbon atoms within the brain cells. This approach helps scientists understand how the brain utilizes alternative energy sources under specific conditions, potentially providing insights into various neurological disorders [].

Sodium pyruvate-(13-C)3, also known as sodium pyruvate enriched with three carbon-13 atoms, is a stable isotope-labeled version of pyruvate. Pyruvate is a key intermediate molecule in cellular metabolism, playing a central role in glycolysis, the breakdown of glucose for energy. The carbon-13 enrichment allows researchers to track the fate of pyruvate in metabolic pathways using techniques like nuclear magnetic resonance (NMR) spectroscopy [].

Molecular Structure Analysis

Sodium pyruvate-(13-C)3 consists of a pyruvate anion (CH3-13C(=O)-CO2-) linked to a sodium cation (Na+). The key features include the carbonyl group (C=O), responsible for its reactivity, and the three enriched carbon-13 atoms (13C) highlighted in the formula. These 13C atoms create a distinct signal in NMR, allowing researchers to differentiate them from naturally abundant carbon-12 atoms [].

Chemical Reactions Analysis

CH3-13C(=O)-CO2- + CoA + NAD+ -> Acetyl-CoA + CO2 + NADH []

(CoA: Coenzyme A, NAD+: Nicotinamide adenine dinucleotide)

Physical And Chemical Properties Analysis

Specific data for Sodium pyruvate-(13-C)3 is limited, but general properties of unlabeled sodium pyruvate can be referenced:

• Melting point: > 300°C (decomposition) []
• Solubility: Highly soluble in water []
• Stability: Stable as a solid, hygroscopic (absorbs moisture) []

Sodium pyruvate-(13-C)3 acts as a tracer molecule in metabolic studies. When introduced into a cell culture or organism, it becomes incorporated into metabolic pathways. Researchers can then use NMR to track the incorporation of the 13C label into downstream metabolites, revealing the fate of pyruvate within the system [].

Case Study: Studying Brain Metabolism

One application of Sodium pyruvate-(13-C)3 involves investigating brain metabolism. Exogenous (added from outside) pyruvate can be taken up by brain cells and contribute to energy production. By using Sodium pyruvate-(13-C)3, researchers can trace the utilization of pyruvate in the brain, providing insights into its role in supporting neuronal function [].